To calculate result you have to disable your ad blocker first.
калькулятор производных
Введите функцию и переменную, чтобы найти производную с помощью калькулятор производных.
производная онлайн
калькулятор производных используется для нахождения производной заданной функции по независимой переменной. Этот калькулятор может выполнить явное дифференцирование всего одним щелчком мыши.
Производная – Определение
Пусть е(х) быть функцией, область определения которой содержит открытый интервал в некоторой точке Икс 0 . Функция е(х) Говорят, что дифференцируемо при Икс 0 , и производная от е(х) в Икс 0 дается:
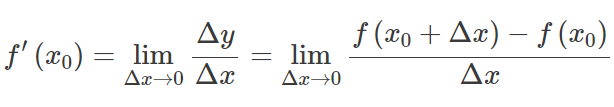
Другими словами, производная измеряет чувствительность к изменению значения функции по отношению к изменению ее аргумента. Обратная функция производной известна как первообразная.
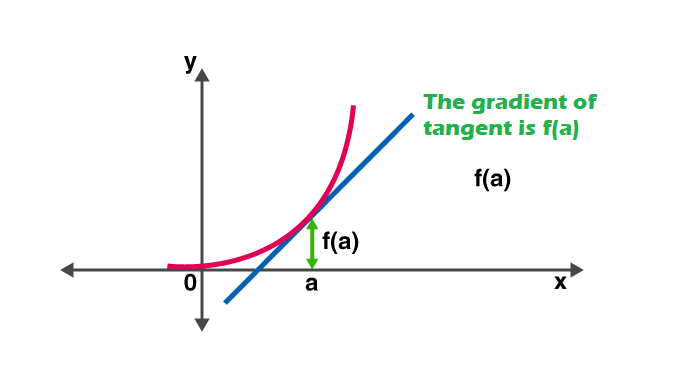
Правила производной
Вот несколько правил дифференциации:
Правило мощности
| f(x) | f'(x) |
| xn | nxn-1 |
Экспоненциальные правила
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Логарифмические правила
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Тригонометрические правила
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Правила дифференциации
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Вы можете получить помощь из вышеуказанного калькулятора для решения проблем дифференциации в соответствии с вышеупомянутыми правилами.
Как найти производные с помощью правил?
Воспользуйтесь нашим калькулятор производных с инструкциями по дифференцированию функций в соответствии с правилами дифференцирования. Вот пример руководства для дифференцирование функции используя правила.
Пример
Найдите производную данной функции по «u».
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Решение
Шаг 1: Примените d/du к данной функции.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Шаг 2: Используйте правило, чтобы дифференцировать вышеуказанное выражение.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Шаг 3: Найдите производные
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ по правилу сумм
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Шаг 4: Теперь подставим приведенные выше результаты в (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Следовательно,
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Примеры производных инструментов
Вот несколько примеров производных, решенных с помощью нашего калькулятора дифференцирования.
| Функция | Производная функции |
| производная от х | 1 |
| производная от 3^x | 3x * ln(3) |
| производная от x^2 | 2x |
| производная от x^1/2 | 1/x1/2 |
| производная от 5^x | 5x * ln(5) |
| производная x/2 | 1/2 |
| производная от x^e | e * xe-1 |
| производная от 1/x | -1/x2 |
| производная 2x | 2 |
| производная от 2 | 0 |
| производная от х^х | xx(ln(x) + 1) |
| производная от x^-1 | -x-2 |
| производная от 2^x | 2x * ln(2) |
| производная от 4^x | 4x * ln(4) |
Вы можете перепроверить приведенный выше результат, используя наш калькулятор производных.

