To calculate result you have to disable your ad blocker first.
kalkulator pochodnych
Wprowadź funkcję i zmienną, aby znaleźć pochodną za pomocą kalkulatora pochodnego.
kalkulator pochodnych
Kalkulator pochodnej służy do znalezienia pochodnej danej funkcji względem zmiennej niezależnej. Ten kalkulator może dokonać wyraźnego różnicowania za pomocą jednego kliknięcia.
Pochodna – Definicja
Niech k(x) być funkcją, której dziedzina zawiera w pewnym momencie przedział otwarty X 0 . Funkcja k(x) mówi się, że jest różniczkowalna w X 0 , oraz pochodną k(x) w X 0 jest podawany przez:
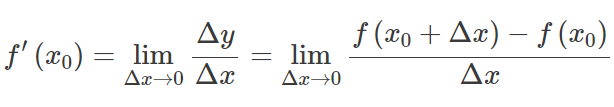
Innymi słowy, pochodna mierzy wrażliwość na zmianę wartości funkcji ze względu na zmianę jej argumentu. Odwrotna funkcja pochodnej jest znana jako funkcja pierwotna.
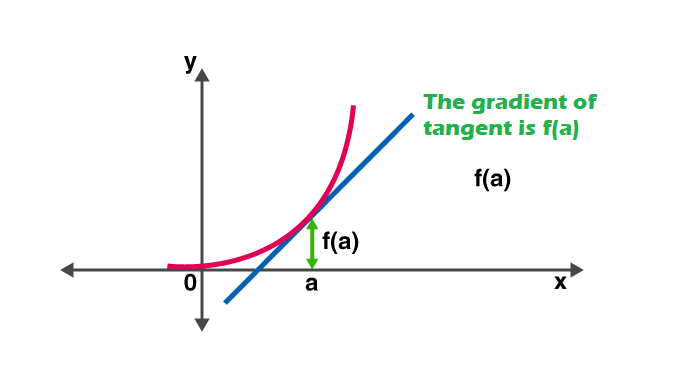
Zasady instrumentu pochodnego
Oto kilka zasad różnicowania:
Zasada mocy
| f(x) | f'(x) |
| xn | nxn-1 |
Reguły wykładnicze
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Reguły logarytmiczne
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Zasady trygonometryczne
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Zasady różnicowania
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Możesz skorzystać z pomocy powyższego kalkulatora różniczkującego, aby rozwiązać problemy z różnicowaniem zgodnie z omówionymi powyżej zasadami.
Jak znaleźć instrumenty pochodne za pomocą reguł?
Skorzystaj z naszego kalkulatora pochodnych z krokami różniczkowania funkcji zgodnie z regułami różniczkowania. Oto przykładowy podręcznik różniczkowanie funkcji za pomocą reguł.
Przykład
Znajdź pochodną danej funkcji po „u”.
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Rozwiązanie
Krok 1: Zastosuj d/du do podanej funkcji.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Krok 2: Aby rozróżnić powyższe wyrażenie, użyj reguły ilorazu.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Krok 3: Znajdź instrumenty pochodne
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ według reguły sumy
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Krok 4: Teraz podstaw powyższe wyniki do (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Dlatego
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Przykłady instrumentów pochodnych
Oto kilka przykładów instrumentów pochodnych rozwiązanych za pomocą naszego kalkulatora różniczkowania.
| Funkcjonować | Pochodna funkcji |
| pochodna x | 1 |
| pochodna 3^x | 3x * ln(3) |
| pochodna x^2 | 2x |
| pochodna x^1/2 | 1/x1/2 |
| pochodna 5^x | 5x * ln(5) |
| pochodna x/2 | 1/2 |
| pochodna x^e | e * xe-1 |
| pochodna 1/x | -1/x2 |
| pochodna 2x | 2 |
| pochodna 2 | 0 |
| pochodna x^x | xx(ln(x) + 1) |
| pochodna x^-1 | -x-2 |
| pochodna 2^x | 2x * ln(2) |
| pochodna 4^x | 4x * ln(4) |
Możesz sprawdzić powyższy wynik, korzystając z naszego kalkulatora instrumentów pochodnych.

