To calculate result you have to disable your ad blocker first.
Derivační kalkulačka
Pomocí derivační kalkulačka zadejte funkci a proměnnou a najděte derivát.
Derivační kalkulačka
Derivační kalkulačka slouží k vyhledání derivace dané funkce vzhledem k nezávisle proměnné. Tato kalkulačka může provádět explicitní rozlišení jediným kliknutím.
Derivát – Definice
Ať f(x) být funkcí, jejíž doména obsahuje v určitém bodě otevřený interval X 0 . Funkce f(x) je prý odlišitelné na X 0 , a derivát z f(x) za X 0 je dán:
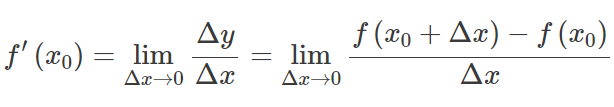
Jinými slovy, derivát měří citlivost na změnu hodnoty funkce s ohledem na změnu jeho argumentu. Reverzní funkce derivace je známá jako primitivní.
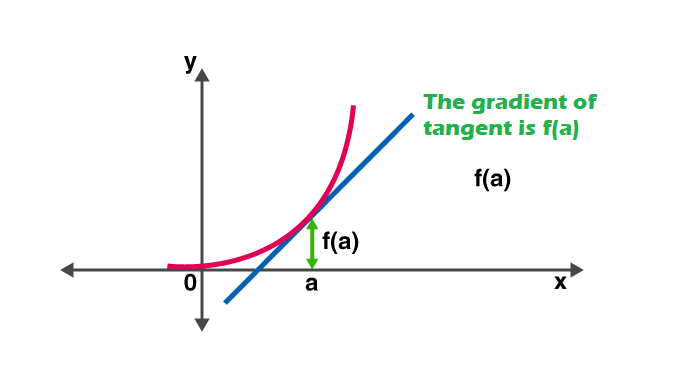
Pravidla derivace
Zde jsou některá pravidla diferenciace:
Pravidlo moci
| f(x) | f'(x) |
| xn | nxn-1 |
Exponenciální pravidla
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Logaritmická pravidla
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Trigonometrická pravidla
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Pravidla diferenciace
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Při řešení problémů s diferenciací podle výše diskutovaných pravidel můžete využít pomoc z výše uvedené diferenciační kalkulačky.
Jak najít deriváty pomocí pravidel?
Použijte naši derivační kalkulačka s kroky k rozlišení funkcí podle rozlišovacích pravidel. Zde je příklad manuálu pro diferencování funkce pomocí pravidel.
Příklad
Najděte derivaci dané funkce vzhledem k „u“.
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Řešení
Krok 1: Použijte d/du na danou funkci.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Krok 2: K odlišení výše uvedeného výrazu použijte pravidlo podílu.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Krok 3: Najděte deriváty
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Krok 4: Nyní nahraďte výše uvedené výsledky v (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Z toho důvodu
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Příklady derivátů
Zde je několik příkladů derivací řešených naší diferenciační kalkulačkou.
| Funkce | Derivace funkce |
| derivace x | 1 |
| derivace 3^x | 3x * ln(3) |
| derivace x^2 | 2x |
| derivace x^1/2 | 1/x1/2 |
| derivace 5^x | 5x * ln(5) |
| derivace x/2 | 1/2 |
| derivát x^e | e * xe-1 |
| derivace 1/x | -1/x2 |
| derivace 2x | 2 |
| derivát 2 | 0 |
| derivace x^x | xx(ln(x) + 1) |
| derivace x^-1 | -x-2 |
| derivace 2^x | 2x * ln(2) |
| derivace 4^x | 4x * ln(4) |
Výše uvedený výsledek můžete zkontrolovat pomocí naší derivační kalkulačka.

