To calculate result you have to disable your ad blocker first.
Afgeleide rekenmachine
Voer de functie en variabele in om de afgeleide te vinden met behulp van de afgeleide rekenmachine.
Afgeleide rekenmachine
Derivatieve rekenmachine wordt gebruikt om de afgeleide van een bepaalde functie te vinden met betrekking tot de onafhankelijke variabele. Deze rekenmachine kan met slechts één klik expliciete differentiatie uitvoeren.
Afgeleide – Definitie
Laat f(x) een functie zijn waarvan het domein op een gegeven moment een open interval bevat X 0 . De functie f(x) Er wordt gezegd dat het differentieerbaar is bij X 0 , en de afgeleide van f(x) bij X 0 wordt gegeven door:
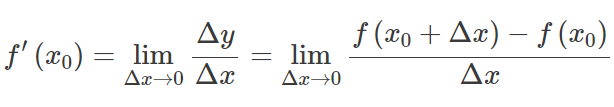
Met andere woorden: de afgeleide meet de gevoeligheid voor een verandering in de functiewaarde met betrekking tot een verandering in zijn argument. De omgekeerde functie van de afgeleide staat bekend als de primitief.
Regels voor afgeleide producten
Hier zijn enkele differentiatieregels:
Machtsregel
| f(x) | f'(x) |
| xn | nxn-1 |
Exponentiële regels
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Logaritmische regels
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Trigonometrische regels
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Differentiatieregels
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
U kunt hulp krijgen van de bovenstaande differentiatiecalculator om differentiatieproblemen op te lossen volgens de hierboven besproken regels.
Hoe vind je derivaten met behulp van regels?
Gebruik onze afgeleide rekenmachine met stappen om de functies te differentiëren volgens de differentiatieregels. Hier is een handmatig voorbeeld voor een functie differentiëren regels gebruiken.
Voorbeeld
Zoek de afgeleide van de gegeven functie met betrekking tot "u".
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Oplossing
Stap 1: Pas d/du toe op de gegeven functie.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Stap 2: Gebruik de quotiëntregel om de bovenstaande uitdrukking te differentiëren.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Stap 3: Vind derivaten
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Stap 4: Vervang nu de bovenstaande resultaten in (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Daarom
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Voorbeelden van derivaten
Hier zijn enkele voorbeelden van derivaten die zijn opgelost door onze differentiatiecalculator.
| Functie | Afgeleide van de functie |
| afgeleide van x | 1 |
| afgeleide van 3^x | 3x * ln(3) |
| afgeleide van x^2 | 2x |
| afgeleide van x^1/2 | 1/x1/2 |
| afgeleide van 5^x | 5x * ln(5) |
| afgeleide van x/2 | 1/2 |
| afgeleide van x^e | e * xe-1 |
| afgeleide van 1/x | -1/x2 |
| afgeleide van 2x | 2 |
| afgeleide van 2 | 0 |
| afgeleide van x^x | xx(ln(x) + 1) |
| afgeleide van x^-1 | -x-2 |
| afgeleide van 2^x | 2x * ln(2) |
| afgeleide van 4^x | 4x * ln(4) |
U kunt het bovenstaande resultaat controleren met behulp van onze afgeleide rekenmachine.

