To calculate result you have to disable your ad blocker first.
Derivative Calculator
Enter the function, select variable, and click calculate button to find the derivative using derivative calculator.
Derivative Calculator With Steps
Derivative calculator is used to find the derivative of a given function with respect to the independent variable. This differentiation calculator can perform explicit differentiation with just one click.
Derivative – Definition
Let f(x) be a function whose domain contains an open interval at some point x0. The function f(x) is said to be differentiable at x0, and the derivative of f(x) at x0 is given by:
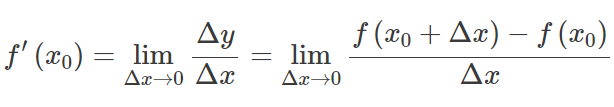
In other words, the derivative measures the sensitivity to a change in the function value with respect to a change in its argument. The reverse function of the derivative is known as the antiderivative.
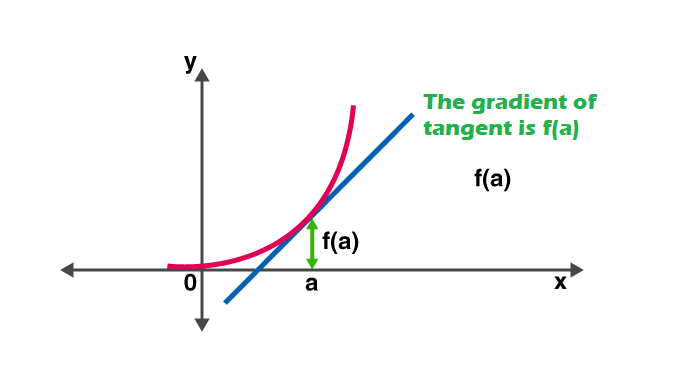
Rules of Derivative
Here are some rules of differentiation:
| Rule name | f(x) | f'(x) |
| Constant | (c) | 0 |
| Sum | f(x) + h(x) | f'(x) + h'(x) |
| Difference | f(x) - h(x) | f'(x) - h'(x) |
| Constant Multiple | f(cx) | c * f'(x) |
| Product | f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| Quotient | f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
| Power | xn | n xn-1 |
Exponential Rules
The exponential rules of differentiation are used for calculating the derivative of exponential functions. The general expressions are:
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Logarithmic Rules
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Trigonometric Rules
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
You can take assistance from the above differentiate calculator to solve differentiation problems according to the above-discussed rules.
How to find derivatives using rules?
Use our derivative calculator with steps to differentiate the functions according to the rules. Here is a manual example for differentiating a function using rules.
Example
Find the derivative of the given function with respect to "u".
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Solution
Step 1: Apply d/du to the given function.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Step 2: Use the quotient rule to differentiate the above expression.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Step 3: Find derivatives
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ by sum rule
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Step 4: Now substitute the above results in (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Hence,
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Examples of derivatives
Here are some examples of derivatives solved by our differentiation calculator.
| Function | Derivative of the function |
| derivative of x | d/dx x = 1 |
| derivative of 3^x | d/dx 3^x = 3x * ln(3) |
| derivative of x^2 | d/dx x^2 = 2x |
| derivative of x^1/2 | d/dx x^1/2 = 1/x1/2 |
| derivative of 5^x | d/dx 5^x = 5x * ln(5) |
| derivative of x/2 | d/dx x/2 = 1/2 |
| derivative of x^e | d/dx x^e = e * xe-1 |
| derivative of 1/x | d/dx 1/x = -1/x2 |
| derivative of 2x | d/dx 2x = 2 |
| derivative of 2 | d/dx 2 = 0 |
| derivative of x^x | d/dx x^x = xx(ln(x) + 1) |
| derivative of x^-1 | d/dx x^-1 = -x-2 |
| derivative of 2^x | d/dx 2^x = 2x * ln(2) |
| derivative of 4^x | d/dx 4^x = 4x * ln(4) |
| derivative of a^x | d/dx a^x = a^x * ln a |
References
- Khan Academy. (n.d.). Derivative – Definition. Khan Academy
- Wikimedia Foundation. (2022, August 28). Differentiation rules. Wikipedia.



