To calculate result you have to disable your ad blocker first.
Calculadora de derivadas
Ingrese la función y la variable para encontrar la derivada usando la calculadora de derivadas.
Calculadora de derivadas con pasos
La calculadora de derivadas se utiliza para encontrar la derivada de una función determinada con respecto a la variable independiente. Esta calculadora de diferenciación puede realizar una diferenciación explícita con solo un clic.
Derivado: Definición
Dejar f(x) ser una función cuyo dominio contenga un intervalo abierto en algún punto X 0 . La función f(x) Se dice que es diferenciable en X 0 , y el derivado de f(x) en X 0 está dada por:
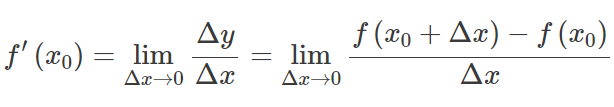
En otras palabras, el derivado Mide la sensibilidad a un cambio en el valor de la función con respecto a un cambio en su argumento. La función inversa de la derivado se conoce como antiderivada.
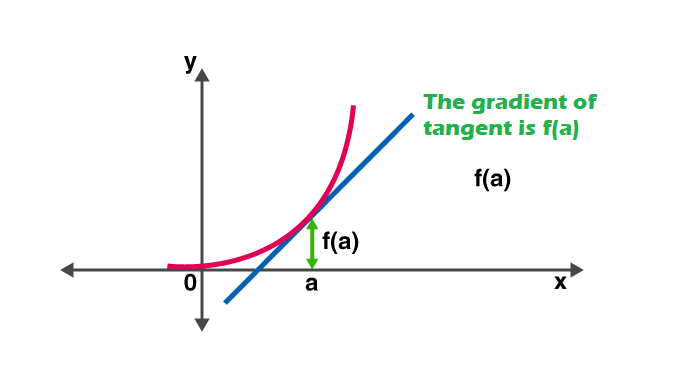
Reglas de derivada
Aquí hay algunas reglas de diferenciación:
| Nombre de la regla | f(x) | f'(x) |
| Constante | (C) | 0 |
| Suma | f(x) + h(x) | f'(x) + h'(x) |
| Diferencia | f(x) - h(x) | f'(x) - h'(x) |
| Múltiple constante | f(cx) | c*f'(x) |
| Producto | f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| Cociente | f(x) / h(x) | 1/h 2 (x)[f'(x) h(x) - h'(x) f(x)] |
| Fuerza | X norte | n x n-1 |
Reglas exponenciales
Las reglas de diferenciación exponencial se utilizan para calcular la derivada de funciones exponenciales. Las expresiones generales son:
| f(x) | f'(x) |
| a X | ln (a) a X |
| mi X | mi X |
Reglas logarítmicas
| f(x) | f'(x) |
| registro a (X) | 1/xln(a) |
| ln|x| | 1/x |
Reglas trigonométricas
| f(x) | f'(x) |
| porque(x) | -pecado(x) |
| pecado (x) | porque(x) |
| tan(x) | segundo 2 (X) |
| Sec (x) | seg(x)tan(x) |
| csc(x) | -csc(x)cuna(x) |
| cuna (x) | -CSC 2 (X) |
Puede obtener ayuda de la calculadora de diferenciación anterior para resolver problemas de diferenciación de acuerdo con las reglas mencionadas anteriormente.
¿Cómo encontrar derivadas usando reglas?
Use nuestra calculadora derivada con pasos para diferenciar las funciones de acuerdo con las reglas. Aquí hay un ejemplo manual para diferenciar una función usando reglas.
Ejemplo
Encuentre la derivada de la función dada con respecto a " tu ".
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Solución
Paso 1: Aplicar d/du a la función dada.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Paso 2: Usa la regla del cociente para derivar la expresión anterior.
$$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Paso 3: encontrar derivadas
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ by sum rule
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Etapa 4: Ahora sustituya los resultados anteriores en (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Por lo tanto,
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Ejemplos de derivados
A continuación se muestran algunos ejemplos de derivadas resueltas con nuestra calculadora de diferenciación.
| Función | Derivada de la función |
| derivado de X | 1 |
| derivado de 3^x | 3x * ln(3) |
| derivado de x^2 | 2x |
| derivado de x^1/2 | 1/x 1/2 |
| derivado de 5^x | 5x * ln(5) |
| derivado de x/2 | 1/2 |
| derivado de x^e | y *x e-1 |
| derivado de 1/x | -1/x 2 |
| derivado de 2x | 2 |
| derivado de 2 | 0 |
| derivado de x^x | xx(ln(x) + 1) |
| derivado de x^-1 | -X -2 |
| derivado de 2^x | 2x * ln(2) |
| derivado de 4^x | 4x * ln(4) |

