To calculate result you have to disable your ad blocker first.
미분계산기
도함수 계산기를 사용하여 도함수를 구하는 함수와 변수를 입력합니다.
Table of Contents:
파생 계산기
미분 계산기는 독립 변수에 대해 주어진 함수의 미분을 찾는 데 사용됩니다. 이 계산기는 단 한 번의 클릭으로 명시적인 미분을 수행할 수 있습니다.
파생상품 – 정의
하자 에프엑스(f(x)) 특정 지점에서 열린 간격을 포함하는 도메인을 갖는 함수여야 합니다. 엑스 0 . 기능 에프엑스(f(x)) 는 에서 미분 가능하다고 합니다. 엑스 0 , 및 의 파생어 에프엑스(f(x)) at 엑스 0 는 다음과 같이 제공됩니다.
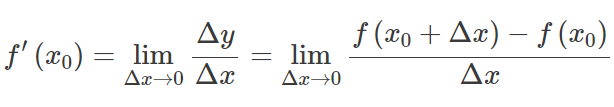
즉, 미분은 인수 변경에 따른 함수 값 변경에 대한 민감도를 측정합니다. 미분의 역함수는 역도함수.
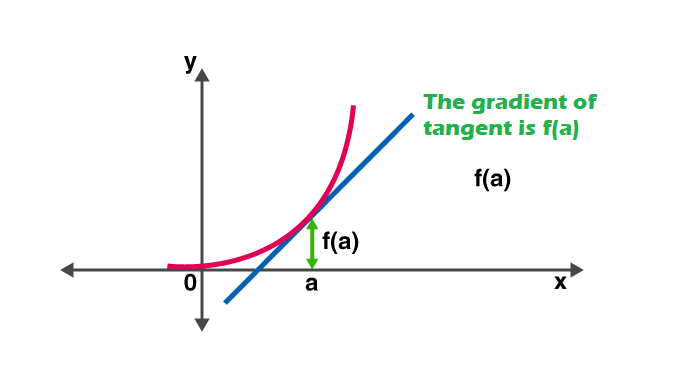
파생 규칙
다음은 몇 가지 차별화 규칙입니다.
권력의 법칙
| f(x) | f'(x) |
| xn | nxn-1 |
지수 규칙
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
로그 규칙
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
삼각법 규칙
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
차별화 규칙
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
위의 차별화 계산기에서 도움을 받아 위에서 논의 된 규칙에 따라 분화 문제를 해결할 수 있습니다.
규칙을 사용하여 파생 상품을 찾는 방법은 무엇입니까?
미분 규칙에 따라 기능을 미분하는 단계가 포함된 미분 계산기를 사용하세요. 다음은 수동 예제입니다. 기능 차별화 규칙을 사용합니다.
예
'u'에 대해 주어진 함수의 도함수를 찾습니다.
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
해결책
1 단계: 주어진 함수에 d/du를 적용합니다.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
2 단계: 위 식을 구별하려면 몫의 법칙을 사용하세요.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
3단계: 파생 상품 찾기
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ 합계 규칙에 따라
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
4단계: 이제 위의 결과를 (1)에 대입합니다.
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
따라서
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
파생상품의 예
다음은 미분 계산기로 해결한 미분의 몇 가지 예입니다.
| 기능 | 함수의 파생 |
| x의 파생물 | 1 |
| 3^x의 미분 | 3x * ln(3) |
| x^2의 미분 | 2x |
| x^1/2의 미분 | 1/x1/2 |
| 5^x의 도함수 | 5x * ln(5) |
| x/2의 미분 | 1/2 |
| x^e의 미분 | e * xe-1 |
| 1/x의 미분 | -1/x2 |
| 2x의 파생물 | 2 |
| 2의 파생물 | 0 |
| x^x의 파생물 | xx(ln(x) + 1) |
| x^-1의 미분 | -x-2 |
| 2^x의 도함수 | 2x * ln(2) |
| 4^x의 도함수 | 4x * ln(4) |
파생 계산기를 사용하여 위의 결과를 교차 확인할 수 있습니다.

