To calculate result you have to disable your ad blocker first.
حاسبة مشتقة
أدخل الدالة والمتغير لإيجاد المشتق باستخدام الآلة الحاسبة المشتقة.
حاسبة المشتقات
يتم استخدام حاسبة المشتقات للعثور على مشتق دالة معينة بالنسبة للمتغير المستقل. يمكن لهذه الآلة الحاسبة إجراء تمييز واضح بنقرة واحدة فقط.
مشتق ونداش؛ تعريف
دع و (خ) تكون دالة يحتوي مجالها على فاصل زمني مفتوح عند نقطة ما س 0 . الوظيفة و (خ) يُقال أنه مختلف في س 0 , و مشتق من و (خ) في س 0 يتم تقديمه بواسطة:
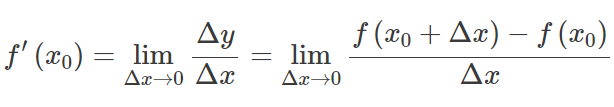
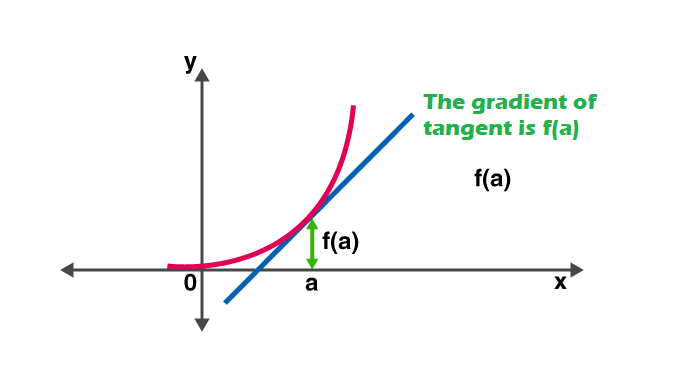
بمعنى آخر، يقيس المشتق مدى الحساسية للتغيير في قيمة الدالة فيما يتعلق بالتغيير في وسيطتها. تُعرف الوظيفة العكسية للمشتق باسم مشتق مضاد.
قواعد المشتقات
فيما يلي بعض قواعد التمايز:
قاعدة القوة
| f(x) | f'(x) |
| xn | nxn-1 |
القواعد الأسية
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
القواعد اللوغاريتمية
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
القواعد المثلثية
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
قواعد التمايز
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
&نبسب;
يمكنك الحصول على المساعدة من حاسبة التفاضل أعلاه لحل مشكلات التفاضل وفقًا للقواعد التي تمت مناقشتها أعلاه.
كيفية العثور على المشتقات باستخدام القواعد؟
استخدم حاسبة المشتقات الخاصة بنا مع الخطوات للتمييز بين الدوال وفقًا لقواعد التمايز. هنا مثال يدوي ل تمييز وظيفة باستخدام القواعد.
مثال
أوجد مشتقة الدالة المعطاة بالنسبة إلى "u".
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
حل
الخطوة 1: قم بتطبيق d/du على الوظيفة المحددة.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
الخطوة 2: استخدم قاعدة القسمة للتمييز بين التعبير أعلاه.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
الخطوه 3: البحث عن المشتقات
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
الخطوة 4: الآن استبدل النتائج المذكورة أعلاه في (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
ومن ثم
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
أمثلة على المشتقات
فيما يلي بعض الأمثلة على المشتقات التي تم حلها بواسطة حاسبة التفاضل الخاصة بنا.
| وظيفة | مشتق من الوظيفة |
| مشتق من x | 1 |
| مشتق من 3^x | 3x * ln(3) |
| مشتق من x^2 | 2x |
| مشتقة x^1/2 | 1/x1/2 |
| مشتق من 5^x | 5x * ln(5) |
| مشتق من س/2 | 1/2 |
| مشتق من x^e | e * xe-1 |
| مشتق من 1/س | -1/x2 |
| مشتق من 2x | 2 |
| مشتق من 2 | 0 |
| مشتق من x^x | xx(ln(x) + 1) |
| مشتق من x^-1 | -x-2 |
| مشتق من 2^x | 2x * ln(2) |
| مشتق من 4^x | 4x * ln(4) |
يمكنك التحقق من النتيجة المذكورة أعلاه باستخدام حاسبة المشتقات الخاصة بنا.

