To calculate result you have to disable your ad blocker first.
Ableitungsrechner
Geben Sie die Funktion und Variable ein, um die Ableitung mit dem Ableitungsrechner zu ermitteln.
Ableitungsrechner
Der Ableitungsrechner wird verwendet, um die Ableitung einer gegebenen Funktion in Bezug auf die unabhängige Variable zu finden. Dieser Rechner kann mit nur einem Klick eine explizite Differenzierung durchführen.
Derivat – Definition
Lassen Sie f(x) eine Funktion sein, deren Domäne irgendwann ein offenes Intervall enthält X 0 . Die Funktion f(x) soll differenzierbar bei X 0 , und die Ableitung von f(x) bei X 0 ist gegeben durch:
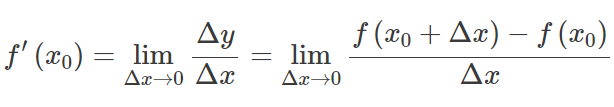
Mit anderen Worten: Die Ableitung misst die Empfindlichkeit gegenüber einer Änderung des Funktionswerts in Bezug auf eine Änderung seines Arguments. Die Umkehrfunktion der Ableitung wird als Stammfunktion.
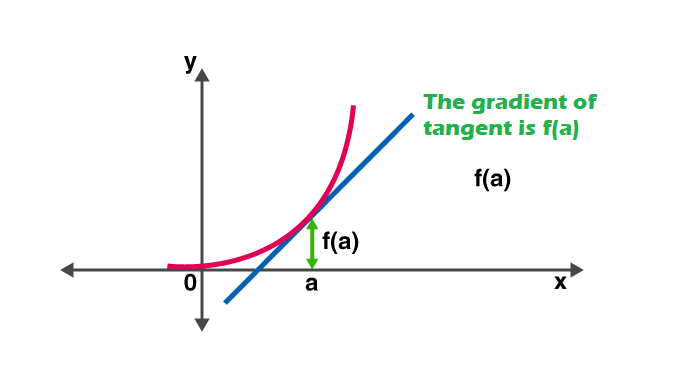
Regeln der Ableitung
Hier einige Regeln zur Differenzierung:
Machtregel
| f(x) | f'(x) |
| xn | nxn-1 |
Exponentielle Regeln
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Logarithmische Regeln
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Trigonometrische Regeln
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Differenzierungsregeln
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Sie können den oben genannten Differenzierungsrechner nutzen, um Differenzierungsprobleme gemäß den oben besprochenen Regeln zu lösen.
Wie finde ich Derivate mithilfe von Regeln?
Nutzen Sie unseren Ableitungsrechner mit Schritten, um die Funktionen gemäß den Differenzierungsregeln zu differenzieren. Hier ist ein manuelles Beispiel für eine Funktion differenzieren Regeln anwenden.
Beispiel
Finden Sie die Ableitung der gegebenen Funktion nach „u“.
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Lösung
Schritt 1: Wenden Sie d/du auf die angegebene Funktion an.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Schritt 2: Verwenden Sie die Quotientenregel, um den obigen Ausdruck zu differenzieren.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Schritt 3: Finden Sie Derivate
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Schritt 4: Ersetzen Sie nun die obigen Ergebnisse in (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Daher
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Beispiele für Derivate
Hier sind einige Beispiele für Ableitungen, die mit unserem Differenzierungsrechner gelöst werden.
| Funktion | Ableitung der Funktion |
| Ableitung von x | 1 |
| Ableitung von 3^x | 3x * ln(3) |
| Ableitung von x^2 | 2x |
| Ableitung von x^1/2 | 1/x1/2 |
| Ableitung von 5^x | 5x * ln(5) |
| Ableitung von x/2 | 1/2 |
| Ableitung von x^e | e * xe-1 |
| Ableitung von 1/x | -1/x2 |
| Ableitung von 2x | 2 |
| Ableitung von 2 | 0 |
| Ableitung von x^x | xx(ln(x) + 1) |
| Ableitung von x^-1 | -x-2 |
| Ableitung von 2^x | 2x * ln(2) |
| Ableitung von 4^x | 4x * ln(4) |
Sie können das obige Ergebnis mit unserem Ableitungsrechner überprüfen.

