To calculate result you have to disable your ad blocker first.
Calculateur de dérivée
Entrez la fonction et la variable pour trouver la dérivée à l'aide de la calculateur de dérivée.
Calculateur de dérivée
Le calculateur de dérivée est utilisé pour trouver la dérivée d'une fonction donnée par rapport à la variable indépendante. Cette calculatrice peut effectuer une différenciation explicite en un seul clic.
Dérivé - Définition
Laissez f(x) être une fonction dont le domaine contient un intervalle ouvert à un moment donné X 0 . La fonction f(x) est dit différentiable à X 0 , et le dérivé de f(x) à X 0 est donné par :
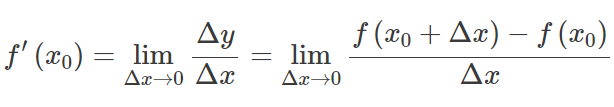
En d'autres termes, la dérivée mesure la sensibilité à un changement de la valeur de la fonction par rapport à un changement de son argument. La fonction inverse de la dérivée est connue sous le nom de primitive.
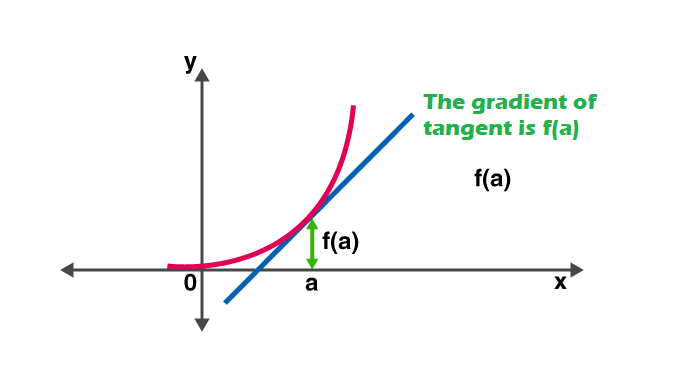
Règles de dérivée
Voici quelques règles de différenciation :
Règle de puissance
| f(x) | f'(x) |
| xn | nxn-1 |
Règles exponentielles
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Règles logarithmiques
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Règles trigonométriques
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Règles de différenciation
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Vous pouvez bénéficier de l'aide du calculateur de différenciation ci-dessus pour résoudre les problèmes de différenciation selon les règles évoquées ci-dessus.
Comment trouver des dérivés en utilisant des règles?
Utilisez notre calculateur de dérivées avec des étapes pour différencier les fonctions selon les règles de différenciation. Voici un exemple manuel pour différencier une fonction en utilisant des règles.
Exemple
Trouvez la dérivée de la fonction donnée par rapport à "u".
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Solution
Étape 1: Appliquer d/du à la fonction donnée.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Étape 2: Utilisez la règle du quotient pour différencier l’expression ci-dessus.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Étape 3: Trouver des produits dérivés
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ par règle de somme
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Étape 4: Remplacez maintenant les résultats ci-dessus par (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Par conséquent,
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Exemples de dérivés
Voici quelques exemples de dérivées résolues par notre calculateur de différenciation.
| Fonction | Dérivée de la fonction |
| dérivée de x | 1 |
| dérivée de 3^x | 3x * ln(3) |
| dérivée de x ^ 2 | 2x |
| dérivée de x ^ 1/2 | 1/x1/2 |
| dérivée de 5^x | 5x * ln(5) |
| dérivée de x/2 | 1/2 |
| dérivée de x^e | e * xe-1 |
| dérivée de 1/x | -1/x2 |
| dérivée de 2x | 2 |
| dérivée de 2 | 0 |
| dérivée de x^x | xx(ln(x) + 1) |
| dérivée de x^-1 | -x-2 |
| dérivée de 2^x | 2x * ln(2) |
| dérivée de 4^x | 4x * ln(4) |
Vous pouvez recouper le résultat ci-dessus en utilisant notre calculateur de dérivée.

