To calculate result you have to disable your ad blocker first.
kalkulator turunan
Masukkan fungsi dan variabel untuk mencari turunannya menggunakan kalkulator turunan.
Kalkulator Derivatif
Kalkulator turunan digunakan untuk mencari turunan suatu fungsi tertentu terhadap variabel bebas. Kalkulator ini dapat melakukan diferensiasi eksplisit hanya dengan satu klik.
Derivatif – Definisi
Mari f(x) menjadi fungsi yang domainnya berisi interval terbuka pada titik tertentu X 0 . Fungsinya f(x) dikatakan dapat dibedakan di X 0 , dan turunan dari f(x) di X 0 diberikan oleh:
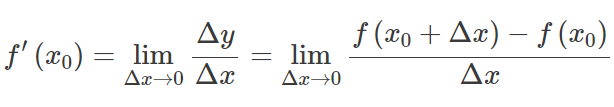
Dengan kata lain, turunan mengukur sensitivitas terhadap perubahan nilai fungsi sehubungan dengan perubahan argumennya. Fungsi kebalikan dari turunannya disebut antiturunan.
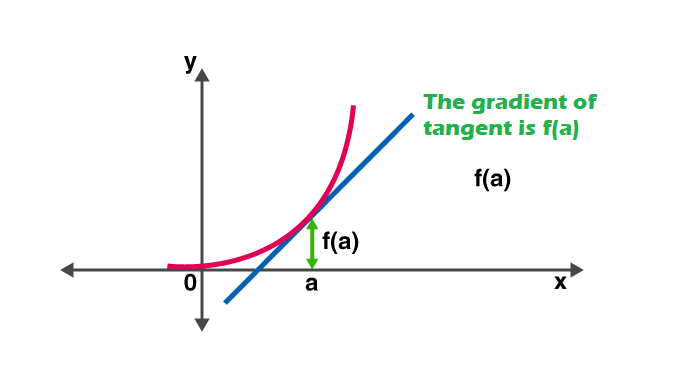
Aturan Derivatif
Berikut adalah beberapa aturan diferensiasi:
Aturan Kekuasaan
| f(x) | f'(x) |
| xn | nxn-1 |
Aturan Eksponensial
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Aturan Logaritma
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Aturan Trigonometri
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Aturan Diferensiasi
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Anda dapat mengambil bantuan dari kalkulator diferensiasi di atas untuk menyelesaikan masalah diferensiasi sesuai dengan aturan yang dibahas di atas.
Bagaimana cara mencari turunan menggunakan aturan?
Gunakan kalkulator turunan kami yang berisi langkah-langkah untuk membedakan fungsi sesuai dengan aturan diferensiasi. Berikut adalah contoh manual untuk membedakan suatu fungsi menggunakan aturan.
Contoh
Temukan turunan dari fungsi yang diberikan terhadap "u".
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Larutan
Langkah 1: Terapkan d/du ke fungsi yang diberikan.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Langkah 2: Gunakan aturan hasil bagi untuk membedakan ekspresi di atas.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Langkah 3: Temukan turunannya
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ menurut aturan penjumlahan
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Langkah 4: Sekarang substitusikan hasil di atas ke (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Oleh karena itu,
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Contoh turunan
Berikut beberapa contoh turunan yang diselesaikan dengan kalkulator diferensiasi kami.
| Fungsi | Turunan dari fungsi |
| turunan dari x | 1 |
| turunan dari 3^x | 3x * ln(3) |
| turunan dari x^2 | 2x |
| turunan dari x^1/2 | 1/x1/2 |
| turunan dari 5^x | 5x * ln(5) |
| turunan dari x/2 | 1/2 |
| turunan dari x^e | e * xe-1 |
| turunan dari 1/x | -1/x2 |
| turunan dari 2x | 2 |
| turunan dari 2 | 0 |
| turunan dari x^x | xx(ln(x) + 1) |
| turunan dari x^-1 | -x-2 |
| turunan dari 2^x | 2x * ln(2) |
| turunan dari 4^x | 4x * ln(4) |
Anda dapat memeriksa silang hasil di atas dengan menggunakan kalkulator turunan kami.

