To calculate result you have to disable your ad blocker first.
Standart Sapma Hesaplama
Standart sapma hesaplayıcısını kullanarak standart sapmayı bulmak için verilen giriş kutusuna örnek veya popülasyon verilerini girin.
Standart sapma hesaplayıcısı
Standart sapma hesaplayıcısı standart sapmayı bulmak için kullanılır, varyans , ortalama ve istatistiksel kareler toplamı. Bu sapma hesaplayıcısı, bir örnek ve popülasyon veri değerleri kümesi alır.
Standart sapma nedir?
Veri dağılımının yayılma ölçüsü şu şekilde bilinir: standart sapma . Her veri gözlemi ile ortalama arasındaki mesafeyi ölçer. Standart sapma iki türdür:
- Örnek standart sapması
- Nüfus standart sapması
Verilen veri kendi popülasyonu ise, kareler toplamını şuna bölün: N .
Verilen veriler daha büyük bir popülasyondan alınan bir örnekse, kareler toplamı şuna bölünmelidir: n – 1 .
Standart sapma formülü
Popülasyon standart sapmasının formülü şu şekildedir:
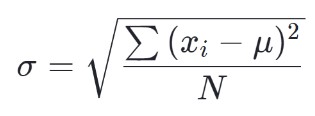
Örnek standart sapmanın formülü şöyledir:
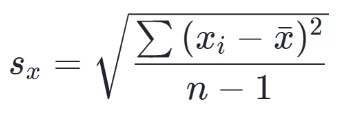
Standart sapma nasıl hesaplanır?
Aşağıda standart sapmanın nasıl hesaplanacağını anlamak için birkaç çözülmüş örnek bulunmaktadır.
Örnek 1: Popülasyon standart sapması için
Nüfus standart sapmasını bulun 8, 22, 26, 25, 30, Ve 33 .
Çözüm
Adım I: Bul Anlam Verilen nüfus verilerine göre
Nüfus verilerinin ortalaması = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Adım II: Şimdi her bir veri noktasının tipik mesafesini bulun ve her sapmanın ortalaması ve karesi.
| Veri değerleri (x Ben ) | X Ben - &mikro; | (X Ben - &mikro;) 2 |
| 8 | 8 - 24 = -16 | (-16) 2 = 256 |
| 22 | 22 - 24 = -2 | (-2) 2 = 4 |
| 26 | 26 - 24 = 2 | (2) 2 = 4 |
| 25 | 25 - 24 = 1 | (1) 2 = 1 |
| 30 | 30 - 24 = 6 | (6) 2 = 36 |
| 33 | 33 - 24= 9 | (9) 2 = 81 |
Adım III: İstatistiksel kareler toplamını bulmak için sapmaları ekleyin.
Σ(xi - &mikro;) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ(xi - &mikro;) 2 = 382
Adım IV: Şimdi kareler toplamını şuna bölün: N .
Σ(xi - &mikro;) 2 /n = 382/6
Σ(xi - &mikro;) 2 /n = 63.667
Adım V: Karekökünü alın.
√[Σ(xi - µ) 2 /n] = &radik;63,667
√[Σ(xi - µ) 2 /n] = 7,979
Bu sorunu hızlı bir şekilde çözmek için yukarıdaki popülasyon standart sapması hesaplayıcısını kullanın.
Örnek 2: Örnek standart sapması için
Örnek standart sapmasını bulun 12, 15, 18, 20, 25 .
Çözüm
Adım I: Verilen örnek verilerin ortalamasını bulun.
Örnek verilerin ortalaması = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Adım II: Şimdi her veri noktasının tipik mesafesini bulun ve her sapmanın ortalaması ve karesi.
| Veri değerleri (x Ben ) | x Ben - X | (X Ben - X) 2 |
| 12 | 12 - 18 = -6 | (-6) 2 = 36 |
| 15 | 15 - 18 = -3 | (-3) 2 = 9 |
| 18 | 18 - 18 = 0 | (0) 2 = 0 |
| 20 | 20 - 18 = 2 | (2) 2 = 4 |
| 25 | 25 - 18 = 7 | (7) 2 = 49 |
Adım III: İstatistikleri bulmak için sapmaları ekleyin kareler toplamı .
Σ(xi - x̅) 2 = 36 + 9 + 0 + 4 + 49
Σ(xi - x̅) 2 = 98
Adım IV: Şimdi kareler toplamını şuna bölün: n – 1 .
Σ(xi - x̅) 2 / n-1 = 98/5-1
Σ(xi - x̅) 2 / n-1 = 98/4
Σ(xi - x̅) 2 / n-1 = 24,5
Adım V: Karekökünü al.
√[Σ(xi - x̅) 2 /n-1] = &radik;24,5
√ [σ (xi - x̅) 2 /n-1] = 4,95

