To calculate result you have to disable your ad blocker first.
Calculadora De Desviacion Estandar
Ingrese datos de muestra o población en el cuadro de entrada proporcionado para encontrar la desviación estándar usando la calculadora de desviación estándar.
Calculadora de desviación estándar
La calculadora de desviación estándar se utiliza para encontrar la desviación estándar, diferencia , media y suma estadística de cuadrados. Esta calculadora de desviación toma una muestra y un conjunto de población de valores de datos.
¿Cuál es la desviación estándar?
La medida de la extensión de la distribución de datos se conoce como Desviación Estándar . Mide la distancia entre cada observación de datos y la media. La desviación estándar es de dos tipos:
- Desviación estándar de la muestra
- Desviación estándar de población
Si los datos dados son la población propia, entonces divida la suma de los cuadrados entre norte .
Si los datos dados son una muestra de una población más grande, entonces la suma de los cuadrados debe dividirse por n - 1 Luego luego
Fórmula de desviación estándar
La fórmula para la desviación estándar de la población es:
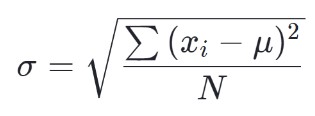
La fórmula para la desviación estándar de la muestra es:
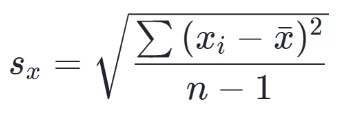
¿Cómo calcular la desviación estándar?
A continuación se muestran algunos ejemplos resueltos para comprender cómo calcular la desviación estándar.
Ejemplo 1: para la desviación estándar de la población
Encuentre la desviación estándar de la población de 8, 22, 26, 25, 30, y 33 .
Solución
Paso I: Encuentra el significar de los datos de población dados.
Media de datos poblacionales = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Paso II: Ahora encuentre la distancia típica de cada punto de datos y la media y el cuadrado de cada desviación.
| Valores de datos (x i ) | X i - µ | (X i -µ) 2 |
| 8 | 8 – 24 = -16 | (-dieciséis) 2 = 256 |
| 22 | 22 – 24 = -2 | (-2) 2 = 4 |
| 26 | 26 – 24 = 2 | (2) 2 = 4 |
| 25 | 25 – 24 = 1 | (1) 2 = 1 |
| 30 | 30 - 24 = 6 | (6) 2 = 36 |
| 33 | 33 – 24= 9 | (9) 2 = 81 |
Paso III: Suma las desviaciones para encontrar la suma estadística de cuadrados.
Σ(xi - µ) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ (xi - μ) 2 = 382
Paso IV: Ahora dividimos la suma de los cuadrados entre norte .
Σ(xi - µ) 2 /norte = 382/6
Σ(xi - µ) 2 /norte = 63,667
Paso V: Saca la raíz cuadrada.
√ [σ (xi - μ) 2 /n] = √63,667
√[Σ(xi - µ) 2 /norte] = 7,979
Utilice la calculadora de desviación estándar de población anterior para resolver este problema rápidamente.
Ejemplo 2: para la desviación estándar de la muestra
Encuentre la desviación estándar muestral de 12, 15, 18, 20, 25 .
Solución
Paso I: Encuentre la media de los datos de muestra dados.
Media de los datos de la muestra = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Paso II: Ahora encuentre la distancia típica de cada punto de datos y la media y el cuadrado de cada desviación.
| Valores de datos (x i ) | x i - x̅ | (X i - X) 2 |
| 12 | 12 – 18 = -6 | (-6) 2 = 36 |
| 15 | 15 – 18 = -3 | (-3) 2 = 9 |
| 18 | 18 – 18 = 0 | (0) 2 = 0 |
| 20 | 20 – 18 = 2 | (2) 2 = 4 |
| 25 | 25 – 18 = 7 | (7) 2 = 49 |
Paso III: Suma las desviaciones para encontrar las estadísticas. suma de cuadrados .
Σ(xi - x̅) 2 = 36 + 9 + 0 + 4 + 49
Σ (xi - x̅) 2 = 98
Paso IV: Ahora dividimos la suma de los cuadrados entre n - 1 Luego luego
Σ(xi - x̅) 2 / n-1 = 98/5-1
Σ (xi - x̅) 2 / n-1 = 98/4
Σ(xi - x̅) 2 / n-1 = 24,5
Paso V: Saca la raíz cuadrada.
√[Σ(xi - x̅) 2 /n-1] = &rad;24,5
√[Σ(xi - x̅) 2 /n-1] = 4.95

