To calculate result you have to disable your ad blocker first.
Calcolo Deviazione Standard
Inserisci i dati del campione o della popolazione nella casella di input fornita per trovare la deviazione standard utilizzando il calcolatore della deviazione standard.
Calcolatore della deviazione standard
Il calcolatore della deviazione standard viene utilizzato per trovare la deviazione standard, varianza , media e somma statistica dei quadrati. Questo calcolatore di deviazione prende un campione e una serie di valori di dati.
Qual è la deviazione standard?
La misura della diffusione della distribuzione dei dati è nota come deviazione standard . Misura la distanza tra ciascuna osservazione dei dati e la media. La deviazione standard è di due tipi:
- Deviazione standard del campione
- Deviazione standard della popolazione
Se i dati forniti rappresentano la popolazione a sé stante, dividi la somma dei quadrati per N .
Se i dati forniti sono un campione di una popolazione più ampia, è necessario dividere la somma dei quadrati per n– 1 .
Formula della deviazione standard
La formula per la deviazione standard della popolazione è:
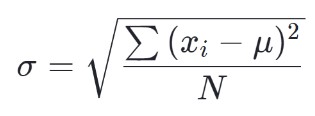
La formula per la deviazione standard del campione è:
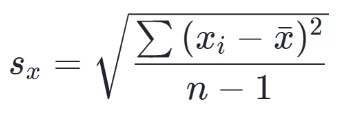
Come calcolare la deviazione standard?
Di seguito sono riportati alcuni esempi risolti per capire come calcolare la deviazione standard.
Esempio 1: per la deviazione standard della popolazione
Trova la deviazione standard della popolazione di 8, 22, 26, 25, 30, E 33 .
Soluzione
Passo I: Trovare il Significare dei dati sulla popolazione forniti.
Media dei dati sulla popolazione = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Passaggio II: Ora trova la distanza tipica di ciascun punto dati e amp; la media e il quadrato di ciascuna deviazione.
| Valori dei dati (x io ) | X io - µ | (X io -µ) 2 |
| 8 | 8 - 24 = -16 | (-16) 2 = 256 |
| 22 | 22 - 24 = -2 | (-2) 2 = 4 |
| 26 | 26 - 24 = 2 | (2) 2 = 4 |
| 25 | 25 - 24 = 1 | (1) 2 = 1 |
| 30 | 30 -24 = 6 | (6) 2 = 36 |
| 33 | 33 - 24=9 | (9) 2 = 81 |
Passaggio III: Aggiungi le deviazioni per trovare la somma statistica dei quadrati.
Σ(xi - µ) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ (xi - μ) 2 = 382
Passaggio IV: Ora dividi la somma dei quadrati N Quindi, quindi
Σ(xi - µ) 2 /n = 382/6
Σ(xi - µ) 2 /n = 63.667
Passaggio V: Prendi la radice quadrata.
√[Σ(xi - µ) 2 /n] = &radical;63.667
√[Σ(xi - µ) 2 /n] = 7,979
Utilizza il calcolatore della deviazione standard della popolazione sopra per risolvere rapidamente questo problema.
Esempio 2: per la deviazione standard del campione
Trova la deviazione standard campionaria di 12, 15, 18, 20, 25 .
Soluzione
Passo I: Trova la media dei dati campione forniti.
Media dei dati campionari = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Passaggio II: Ora trova la distanza tipica di ciascun punto dati e amp; la media e il quadrato di ciascuna deviazione.
| Valori dei dati (x io ) | x io - x̅ | (X io - X) 2 |
| 12 | 12 - 18 = -6 | (-6) 2 = 36 |
| 15 | 15 - 18 = -3 | (-3) 2 = 9 |
| 18 | 18 - 18 = 0 | (0) 2 = 0 |
| 20 | 20 - 18 = 2 | (2) 2 = 4 |
| 25 | 25 - 18 = 7 | (7) 2 = 49 |
Passaggio III: Aggiungi le deviazioni per trovare la statistica somma dei quadrati .
Σ (xi - x̅) 2 = 36 + 9 + 0 + 4 + 49
Σ(xi - x̅) 2 = 98
Passaggio IV: Ora dividi la somma dei quadrati per n– 1 .
Σ(xi - x̅) 2 /n-1 = 98/5-1
Σ(xi - x̅) 2 /n-1 = 98/4
Σ(xi - x̅) 2 /n-1 = 24,5
Passaggio V: Prendi la radice quadrata.
&radical;[Σ(xi - x̅) 2 /n-1] = &radica;24,5
&radical;[Σ(xi - x̅) 2 /n-1] = 4,95

