To calculate result you have to disable your ad blocker first.
標準偏差 計算サイト
指定された入力ボックスにサンプルまたは母集団のデータを入力し、標準偏差計算ツールを使用して標準偏差を求めます。
Table of Contents:
標準偏差計算ツール
標準偏差計算機は標準偏差を見つけるために使用されます。 分散 、平均、および統計的な平方和。この偏差計算ツールは、データ値のサンプルと母集団のセットを取得します。
標準偏差とは何ですか?
データ配布の広がりの尺度は次のように知られています。 標準偏差 。各データ観測値と平均値との間の距離を測定します。標準偏差には 2 つのタイプがあります。
- サンプル標準偏差
- 母集団標準偏差
指定されたデータがそれ自体の母集団である場合、二乗和を次の値で割ります。 N 。
指定されたデータがより大きな母集団からのサンプルである場合、二乗和を次の値で割る必要があります。 – 1 .
標準偏差の式
母集団標準偏差の式は次のとおりです。
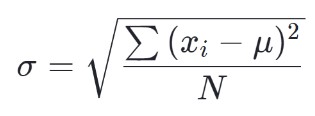
標本の標準偏差の式は次のとおりです。
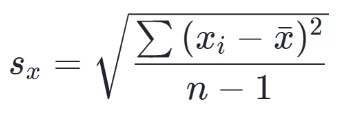
標準偏差を計算するにはどうすればよいですか?
以下に、標準偏差の計算方法を理解するための解決済みの例をいくつか示します。
例 1: 母集団の標準偏差の場合
の母集団標準偏差を求めます。 8、22、26、25、30、 そして 33 。
解決
ステップ 1: を見つける 平均 指定された人口データの。
人口データの平均 = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
ステップ II: 次に、各データポイントの一般的な距離を見つけます。各偏差の平均と二乗。
| データ値 (x 私 ) | バツ 私 - µ | (バツ 私 - µ) 2 |
| 8 | 8– 24 = -16 | (-16) 2 = 256 |
| 22 | 22– 24 = -2 | (-2) 2 = 4 |
| 26 | 26– 24 = 2 | (2) 2 = 4 |
| 25 | 25– 24 = 1 | (1) 2 = 1 |
| 30 | 30– 24 = 6 | (6) 2 = 36 |
| 33 | 33– 24=9 | (9) 2 = 81 |
ステップ III: 偏差を加算して統計的な二乗和を求めます。
Σ(xi - µ) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ(xi - µ) 2 = 382
ステップ IV: 次に平方和を次で割ります。 n 。
Σ(xi - µ) 2 /n = 382/6
Σ(xi - µ) 2 /n = 63.667
ステップ V: 平方根を求めます。
√[Σ(xi - µ) 2 /n] = √63.667
√[Σ(xi - µ) 2 /n] = 7.979
上記の母集団標準偏差計算機を使用して、この問題を迅速に解決します。
例 2: サンプルの標準偏差の場合
のサンプル標準偏差を求めます。 12、15、18、20、25 。
解決策
ステップ 1: 指定されたサンプルデータの平均を求めます。
サンプルデータの平均 = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
ステップ II: 次に、各データポイントの典型的な距離と、各偏差の平均と平均を見つけます。
| データ値 (x 私 ) | x 私 - バツ | (バツ 私 - バツ) 2 |
| 12 | 12– 18 = -6 | (-6) 2 = 36 |
| 15 | 15– 18 = -3 | (-3) 2 = 9 |
| 18 | 18– 18 = 0 | (0) 2 = 0 |
| 20 | 20– 18 = 2 | (2) 2 = 4 |
| 25 | 25– 18 = 7 | (7) 2 = 49 |
ステップ III: 偏差を加算して統計値を求めます 平方和 。
Σ(xi - x̅) 2 = 36 + 9 + 0 + 4 + 49
Σ(xi - x̅) 2 = 98
ステップ IV: 次に、正方形の合計を分割します – 1 。
Σ(xi - x̅) 2 / n-1 = 98/ 5-1
Σ(xi - x̅) 2 / n-1 = 98/4
Σ(xi - x̅) 2 / n-1 = 24.5
ステップV: 平方根を取ります。
√[Σ(xi - x̅) 2 /n-1] = √24.5
√[σ(xi -x̅) 2 /n-1] = 4.95

