To calculate result you have to disable your ad blocker first.
Calcul Ecart Type
Entrez les données d'échantillon ou de population dans la zone de saisie donnée pour calculer un écart type à l'aide du calculateur d'écart type.
Calculateur d'écart type
Le calculateur d'écart type est utilisé pour trouver l'écart type, variance , la moyenne et la somme statistique des carrés. Ce calculateur d'écart prend un échantillon et un ensemble de valeurs de données.
Quel est l’écart type ?
La mesure de la propagation de la distribution des données est connue sous le nom écart-type . Il mesure la distance entre chaque observation des données et la moyenne. L'écart type est de deux types:
- Exemple d'écart type
- Écart type de la population
Si les données fournies correspondent à la population elle-même, divisez la somme des carrés par N .
Si les données fournies proviennent d’un échantillon d’une population plus large, alors la somme des carrés doit être divisée par n - 1 .
Formule ecart type
La formule de l’écart type de la population est la suivante :
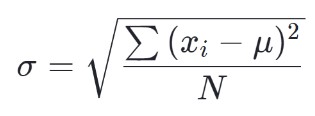
La formule de l'écart type de l'échantillon est :
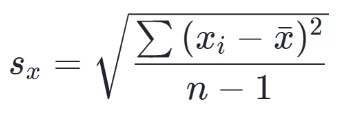
Comment Calculer un écart type ?
Vous trouverez ci-dessous quelques exemples résolus pour comprendre comment calculer l'écart type.
Exemple 1 : Pour l'écart type de la population
Trouver l'écart type de la population de 8, 22, 26, 25, 30, et 33 .
Solution
Étape I: Trouvez le signifier des données démographiques fournies.
Moyenne des données de population = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Étape II : Trouvez maintenant la distance typique de chaque point de données et amp; la moyenne et le carré de chaque écart.
| Valeurs des données (x je ) | X je - µ | (X je - µ) 2 |
| 8 | 8 - 24 = -16 | (-16) 2 = 256 |
| 22 | 22 - 24 = -2 | (-2) 2 = 4 |
| 26 | 26 - 24 = 2 | (2) 2 = 4 |
| 25 | 25 - 24 = 1 | (1) 2 = 1 |
| 30 | 30 - 24 = 6 | (6) 2 = 36 |
| 33 | 33 - 24 = 9 | (9) 2 = 81 |
Étape III : Additionnez les écarts pour trouver la somme statistique des carrés.
Σ(xi - µ) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ(xi - µ) 2 = 382
Étape IV : Divisez maintenant la somme des carrés par n .
Σ(xi - µ) 2 /n = 382/6
Σ(xi - µ) 2 /n = 63,667
Étape V : Prenez la racine carrée.
√[Σ(xi - µ) 2 /n] = √63,667
√[Σ(xi - µ) 2 /n] = 7,979
Utilisez le calculateur d’écart type de population ci-dessus pour résoudre ce problème rapidement.
Exemple 2 : Pour un échantillon d'écart type
Trouver l'écart type de l'échantillon de 12, 15, 18, 20, 25 .
Solution
Étape I : Trouvez la moyenne des exemples de données donnés.
Moyenne des données de l'échantillon = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Étape II : Trouvez maintenant la distance typique de chaque point de données et amp; la moyenne et le carré de chaque écart.
| Valeurs des données (x je ) | x je - x̅ | (X je - X) 2 |
| 12 | 12 - 18 = -6 | (-6) 2 = 36 |
| 15 | 15 - 18 = -3 | (-3) 2 = 9 |
| 18 | 18 - 18 = 0 | (0) 2 = 0 |
| 20 | 20 - 18 = 2 | (2) 2 = 4 |
| 25 | 25 - 18 = 7 | (7) 2 = 49 |
Étape III : Additionnez les écarts pour trouver les statistiques somme des carrés .
Σ (xi - x̅) 2 = 36 + 9 + 0 + 4 + 49
Σ(xi - x̅) 2 = 98
Étape IV : Divisez maintenant la somme des carrés par n - 1 .
Σ(xi - x̅) 2 / n-1 = 98/5-1
Σ(xi - x̅) 2 / n-1 = 98/4
Σ(xi - x̅) 2 / n-1 = 24,5
Étape V : Prenez la racine carrée.
√[Σ(xi - x̅) 2 /n-1] = √24,5
√[Σ(xi - x̅) 2 /n-1] = 4,95

