To calculate result you have to disable your ad blocker first.
Standardabweichung Rechner
Geben Sie Stichproben- oder Populationsdaten in das entsprechende Eingabefeld ein, um die Standardabweichung mithilfe des Standardabweichung rechner zu ermitteln.
Standardabweichung Rechner
Der Standardabweichungsrechner wird verwendet, um die Standardabweichung zu ermitteln. Varianz , Mittelwert und die statistische Summe der Quadrate. Dieser Abweichungsrechner nimmt eine Stichprobe und einen Populationssatz von Datenwerten.
Was ist eine Standardabw Eichung?
Das Maß für die Ausbreitung der Datenverteilung ist bekannt als Standardabweichung . Es misst den Abstand zwischen jeder Datenbeobachtung und dem Mittelwert. Es gibt zwei Arten von Standardabweichungen:
- Standardabweichung der Stichprobe
- Bevölkerungsstandardabweichung
Wenn es sich bei den angegebenen Daten um die eigene Grundgesamtheit handelt, dividieren Sie die Summe der Quadrate durch N .
Wenn es sich bei den angegebenen Daten um eine Stichprobe aus einer größeren Grundgesamtheit handelt, muss die Summe der Quadrate durch geteilt werden n – 1 .
Standardabweichung Formel
Die Formel für die Populationsstandardabweichung lautet:
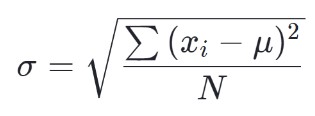
Die Formel für die Stichprobenstandardabweichung lautet:
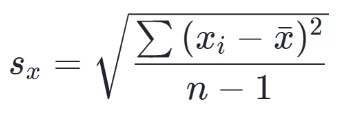
Wie Berechnet man Standardabweichung?
Nachfolgend finden Sie einige gelöste Beispiele, um zu verstehen, wie die Standardabweichung berechnet wird.
Beispiel 1: Für die Standardabweichung der Grundgesamtheit
Ermitteln Sie die Populationsstandardabweichung von 8, 22, 26, 25, 30, Und 33 .
Lösung
Schritt I: Finden Sie die bedeuten der gegebenen Bevölkerungsdaten.
Mittelwert der Bevölkerungsdaten = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Schritt II: Ermitteln Sie nun den typischen Abstand jedes Datenpunkts & der Mittelwert und das Quadrat jeder Abweichung.
| Datenwerte (x ich ) | X ich - µ | (X ich - µ) 2 |
| 8 | 8 – 24 = -16 | (-16) 2 = 256 |
| 22 | 22 – 24 = -2 | (-2) 2 = 4 |
| 26 | 26 – 24 = 2 | (2) 2 = 4 |
| 25 | 25 – 24 = 1 | (1) 2 = 1 |
| 30 | 30 – 24 = 6 | (6) 2 = 36 |
| 33 | 33 - 24 = 9 | (9) 2 = 81 |
Schritt III: Addieren Sie die Abweichungen, um die statistische Summe der Quadrate zu ermitteln.
Σ(xi - µ) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ(xi - µ) 2 = 382
Schritt IV: Teilen Sie nun die Summe der Quadrate durch N .
Σ(xi - µ) 2 /n = 382/6
Σ(xi - µ) 2 /n = 63,667
Schritt V: Ziehe die Quadratwurzel.
√[Σ(xi - µ) 2 /n] = √63,667
√[Σ(xi - µ) 2 /n] = 7,979
Verwenden Sie den obigen Rechner für die Standardabweichung der Grundgesamtheit, um dieses Problem schnell zu lösen.
Beispiel 2: Für die Standardabweichung der Stichprobe
Ermitteln Sie die Stichprobenstandardabweichung von 12, 15, 18, 20, 25 .
Lösung
Schritt I: Ermitteln Sie den Mittelwert der angegebenen Beispieldaten.
Mittelwert der Beispieldaten = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Schritt II: Ermitteln Sie nun den typischen Abstand jedes Datenpunkts & der Mittelwert und das Quadrat jeder Abweichung.
| Datenwerte (x ich ) | x ich - x̅ | (X ich - X) 2 |
| 12 | 12 – 18 = -6 | (-6) 2 = 36 |
| 15 | 15 – 18 = -3 | (-3) 2 = 9 |
| 18 | 18 – 18 = 0 | (0) 2 = 0 |
| 20 | 20 – 18 = 2 | (2) 2 = 4 |
| 25 | 25 – 18 = 7 | (7) 2 = 49 |
Schritt III: Addieren Sie die Abweichungen, um die Statistik zu ermitteln Quadratsumme.
Σ (xi - x̅) 2 = 36 + 9 + 0 + 4 + 49
Σ(xi - x̅) 2 = 98
Schritt IV: Teilen Sie nun die Summe der Quadrate durch n – 1 .
Σ(xi - x̅) 2 / n-1 = 98/5-1
Σ(xi - x̅) 2 / n-1 = 98/4
Σ(xi - x̅) 2 / n-1 = 24,5
Schritt V: Ziehe die Quadratwurzel.
√[Σ(xi - x̅) 2 /n-1] = √24,5
√[Σ(xi - x̅) 2 /n-1] = 4,95

