To calculate result you have to disable your ad blocker first.
Kalkulator deviasi standar
Masukkan data sampel atau populasi ke dalam kotak masukan yang diberikan untuk mencari simpangan baku menggunakan kalkulator simpangan baku.
Kalkulator deviasi standar
Kalkulator simpangan baku digunakan untuk mencari simpangan baku, perbedaan , mean, dan jumlah statistik kuadrat. Kalkulator deviasi ini mengambil kumpulan nilai data sampel dan populasi.
Berapa standar deviasinya?
Ukuran sebaran sebaran data dikenal dengan sebutan deviasi standar . Ini mengukur jarak antara setiap observasi data dan mean. Deviasi standar ada dua jenis:
- Contoh deviasi standar
- Deviasi standar populasi
Jika data yang diberikan adalah populasinya sendiri, bagilah jumlah kuadratnya dengan N .
Jika data yang diberikan merupakan sampel dari populasi yang lebih besar, maka jumlah kuadratnya harus dibagi n – 1 .
Rumus deviasi standar
Rumus simpangan baku populasi adalah:
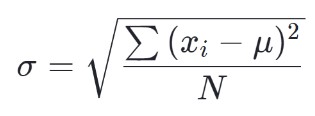
Rumus simpangan baku sampel adalah:
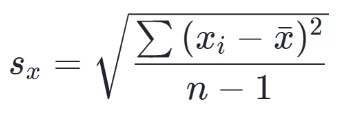
Bagaimana cara menghitung deviasi standar?
Di bawah ini adalah beberapa contoh penyelesaian untuk memahami cara menghitung deviasi standar.
Contoh 1: Untuk standar deviasi populasi
Temukan deviasi standar populasi 8, 22, 26, 25, 30, Dan 33 .
Larutan
Langkah I: Temukan berarti dari data populasi yang diberikan.
Rata-rata data penduduk = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Langkah II: Sekarang temukan jarak khas setiap titik data & mean dan kuadrat setiap deviasi.
| Nilai data (x Saya ) | X Saya - µ | (X Saya - µ) 2 |
| 8 | 8 – 24 = -16 | (-16) 2 = 256 |
| 22 | 22 – 24 = -2 | (-2) 2 = 4 |
| 26 | 26 – 24 = 2 | (2) 2 = 4 |
| 25 | 25 – 24 = 1 | (1) 2 = 1 |
| 30 | 30 – 24 = 6 | (6) 2 = 36 |
| 33 | 33 – 24= 9 | (9) 2 = 81 |
Langkah III: Tambahkan deviasi untuk menemukan jumlah statistik kuadrat.
Σ(xi - µ) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ(xi - µ) 2 = 382
Langkah IV: Sekarang bagilah jumlah kuadratnya dengan N .
Σ(xi - µ) 2 /n = 382/6
Σ(xi - µ) 2 /n = 63.667
Langkah V: Ambil akar kuadratnya.
√[Σ(xi - µ) 2 /n] = √63.667
√[Σ(xi - µ) 2 /n] = 7,979
Gunakan kalkulator deviasi standar populasi di atas untuk menyelesaikan masalah ini dengan cepat.
Contoh 2: Untuk standar deviasi sampel
Temukan simpangan baku sampel dari 12, 15, 18, 20, 25 .
Solusi
Langkah I: Temukan rata -rata data sampel yang diberikan.
Rata-rata data sampel = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Langkah II: Sekarang temukan jarak khas dari setiap titik data & rata -rata dan kuadrat dari setiap penyimpangan.
| Nilai data (x Saya ) | x Saya - x̅ | (X Saya - X) 2 |
| 12 | 12 – 18 = -6 | (-6) 2 = 36 |
| 15 | 15 – 18 = -3 | (-3) 2 = 9 |
| 18 | 18 – 18 = 0 | (0) 2 = 0 |
| 20 | 20-28 = 2 | (2) 2 = 4 |
| 25 | 25 – 18 = 7 | (7) 2 = 49 |
Langkah III: Tambahkan penyimpangan untuk menemukan statistik jumlah kotak .
Σ(xi - x̅) 2 = 36+9+0+4+49
Σ(xi - x̅) 2 = 98
Langkah IV: Sekarang bagilah jumlah kuadratnya dengan n – 1 .
Σ(xi - x̅) 2 / n-1 = 98/ 5-1
Σ(xi - x̅) 2 / n-1 = 98/4
Σ (xi - x̅) 2 / n-1 = 24.5
Langkah V: Ambil akar kuadrat.
√[Σ(xi - x̅) 2 /n-1] = √24.5
√ [σ (xi - x̅) 2 /n-1] = 4,95

