To calculate result you have to disable your ad blocker first.
Antiderivativrechner - Integral
Geben Sie die Funktions-, Variablen-, Ober- und Untergrenze ein. Wählen Sie eine bestimmte oder unbestimmte Integraloption. Klicken Sie auf die Schaltfläche Berechnen, um das Integral mit dem Antiderivativrechner zu finden.
Examples:
Click to evaluate integral
$${\small \int _2^3\:sin\left(x\right)+x/2}$$
$${\small \int _1^2\:cos\:\left(x\right)^{\:2}}$$
$${\small \int _0^1\:x^{\:\left(-1/3\right)}}$$
$${\small \int _1^2\:log\left(\:x\right)}$$
$${\small \int _1^2\:cos\left(x\right)+x^2}$$
$${\small \int _1^3\:e\:^\left(1\:-\:x\right)}$$
Table of Contents:
Der Online-Integralrechner ist ein Tool, das das Integral einer bestimmten Funktion in Bezug auf eine Variable bewertet. Es berechnet auch das bestimmte sowie das unbestimmte Integral für die gegebene Funktion.
Dieser Integralrechner zeigt auch die Integrationsschritte für jede Berechnung an.
Was ist ein Integral?
Ein Integral kann definiert werden als:
"Ein Integral weist Funktionen Funktionen zu, die Volumen, Flächenverschiebung und sogar Wahrscheinlichkeit definieren können. Integral ist die Umkehrfunktion des Derivats, weshalb es allgemein als Antiderivativ bezeichnet wird."
Der Prozess des Findens eines Integrals wird als Integration bezeichnet. Es wird verwendet, um den Bereich unter der Kurve zu finden. Das Symbol für Integration oder Antiderivativ ist ∫.
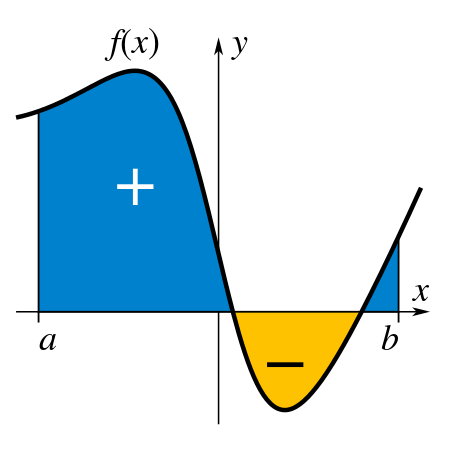
Wie bewerte ich ein Integral?
Beispiel: Bewerten Sie das folgende Integral.
∫ (6x + 2) dx
Lösung:
Schritt 1: Wenden Sie Linearität auf die Funktion an.
= 6 ∫ x dx + 2 ∫ 1 dx ------- 1
Schritt 2: Löse 6 ∫ x dx und 2 ∫ 1 dx getrennt und setze die Werte in die obige Gleichung (1).
6 ∫ x dx
Wenden Sie die Leistungsregel an.
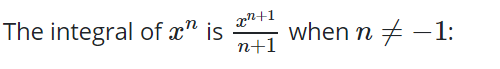
6 ∫ x dx = 6x2 / 2 = 3x2
2 ∫ 1 dx
Wende die konstante Regel ∫a dx = ax + C an.
2 ∫ 1 dx = 2x + C.
Schritt 3: Setzen Sie die gelösten Integrale in Gleichung (1).
= 6 ∫ x dx + 2 ∫ 1 dx
= 3x2 + 2x + C.
Der obige Integrallöser führt alle diese Schritte aus und zeigt Ihnen die vollständige Berechnung für Ihre Einfachheit.
ADVERTISEMENT
