Chat with us
To calculate result you have to disable your ad blocker first.
Antiderivativní kalkulačka
Zadejte funkci, proměnnou, horní a dolní mez. Vyberte jednoznačnou nebo neurčitou integrální možnost. Kliknutím na tlačítko Vypočítat najdete antiderivaci pomocí kalkulačky.
Examples:
Click to evaluate integral
$${\small \int _2^3\:sin\left(x\right)+x/2}$$
$${\small \int _1^2\:cos\:\left(x\right)^{\:2}}$$
$${\small \int _0^1\:x^{\:\left(-1/3\right)}}$$
$${\small \int _1^2\:log\left(\:x\right)}$$
$${\small \int _1^2\:cos\left(x\right)+x^2}$$
$${\small \int _1^3\:e\:^\left(1\:-\:x\right)}$$
Table of Contents:
Online integrální (antiderivativní) kalkulačka je nástroj, který hodnotí integrál dané funkce s ohledem na proměnnou. Rovněž vypočítá určitý i neurčitý integrál pro danou funkci.
Tato integrální kalkulačka také ukazuje kroky integrace pro každý výpočet.
Co je integrál?
Integrál lze definovat jako,
" Integrál přiřazuje funkce funkcím způsobem, který může definovat objem, posunutí oblasti a dokonce pravděpodobnost." Integrál je inverzní funkce derivátu, a proto je obecně označován jako antiderivativní. ”
Proces hledání integrálu je známý jako integrace. Slouží k nalezení oblasti pod křivkou. Symbolem integrace nebo antiderivace je ∫.
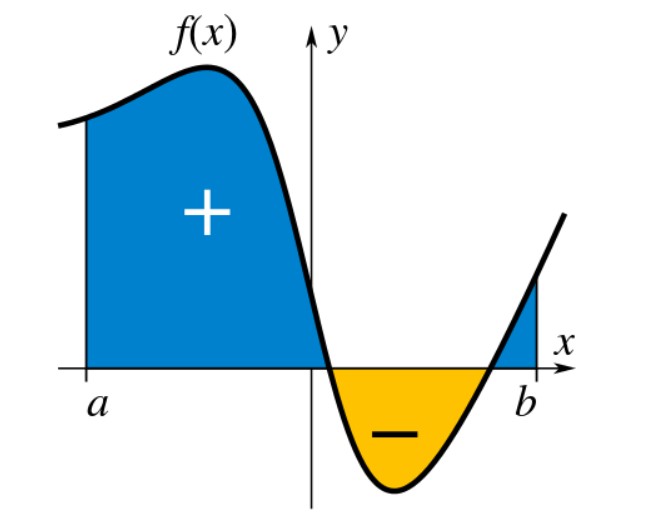
Jak vyhodnotit integrál?
Příklad: Vyhodnoťte následující integrál.
∫ (6x + 2) dx
Řešení:
Krok 1: Aplikujte na funkci linearitu.
= 6 ∫ x dx + 2 ∫ 1 dx ------- 1
Krok 2: Řešení 6 ∫ x dx a 2 ∫ 1 dx odděleně a místo hodnoty výše uvedené rovnice (1).
6 ∫ x dx
Použít pravidlo napájení.
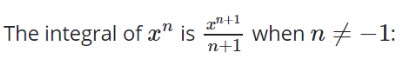
6 ∫ x dx = 6x2/2 = 3x2
2 ∫ 1 dx
Použijte konstantní pravidlo ∫a dx = ax + C.
2 ∫ 1 dx = 2x + C
Krok 3: Řešené integrály vložte do rovnice (1).
= 6 ∫ x dx + 2 ∫ 1 dx
= 3x2 + 2x + C
Integrovaný řešič výše provádí všechny tyto kroky a ukazuje vám kompletní výpočet pro vaši jednoduchost.
ADVERTISEMENT
