To calculate result you have to disable your ad blocker first.
Variance Calculator
To find the variance, select the sample or population option, enter the comma-separated values, and click the calculate button using variance calculator
Variance Calculator with steps
Variance calculator is used to find the variance of sample and population data. This variance solver also finds the standard deviation, the mean, and the statistical sum of squares in one click.
What is a variance?
In statistics, the average of the squared deviations from the mean is said to be the variance. It decides whether the data values are closer or far from the average value.
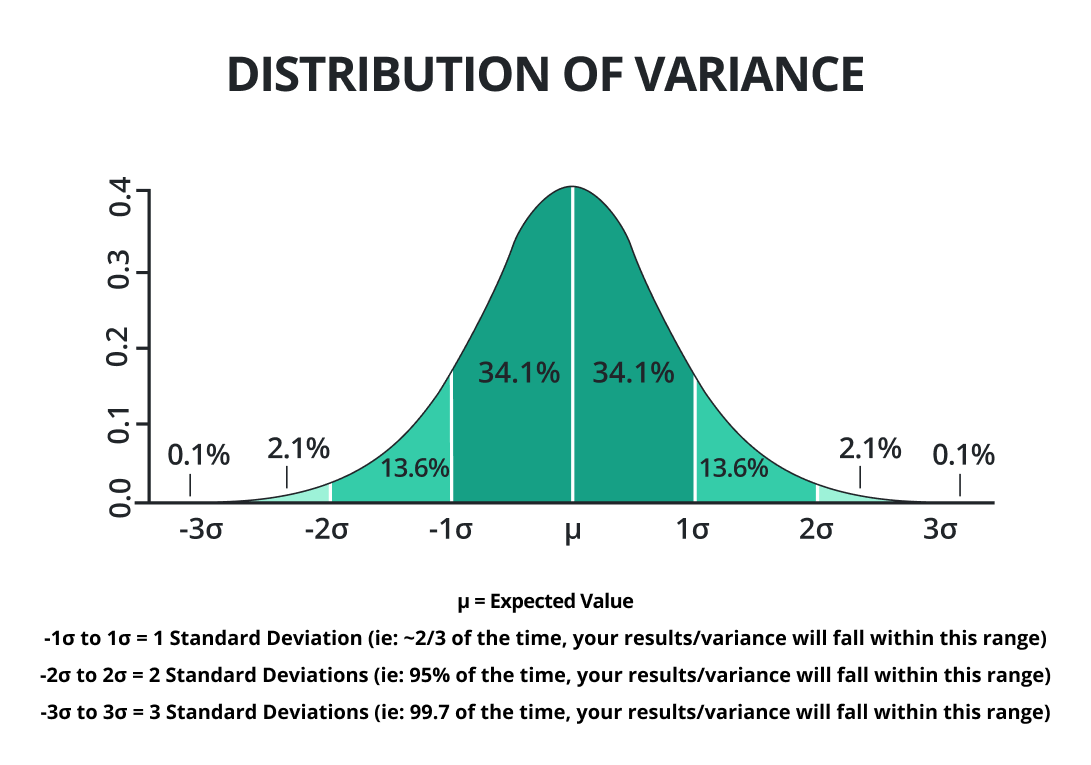
The small variance tells that the random data values are closer to the mean. While the greater variance indicates that the random data values are far from the mean.
Types of variances
- Sample variance
- Population variance
Formulas of variance
The formula for the sample variance is:
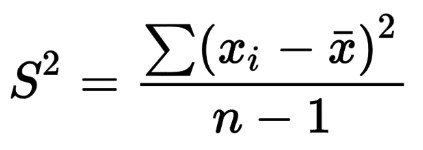
The formula for the population variance is:
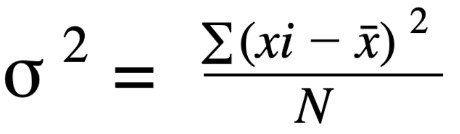
How to calculate variance?
Follow the below examples to learn how to calculate the variance.
Example 1: For sample variance
Find the sample variance of 12, 14, 15, 19, 25.
Solution
Step 1: First of all, calculate the mean of sample data.
Mean = x̅ = Σx/n
= [12 + 14 + 15 + 19 + 25]/5
= 85/5
= 17
Step 2: Now find the difference between each data value from the mean and the square of the differences.
| Data values (x) | xi - x̅ | (xi - x̅)2 |
| 12 | 12 – 17 = -5 | (-5)2 = 25 |
| 14 | 14 – 17 = -3 | (-3)2 = 9 |
| 15 | 15 – 17 = -2 | (-2)2 = 4 |
| 19 | 19 – 17 = 2 | (2)2 = 4 |
| 25 | 25 – 17 = 8 | (8)2 = 64 |
Step 3: Find the statistical sum of squares.
Σ(xi - x̅)2 = 25 + 9 + 4 + 4 + 64
= 106
Step 4: Take the formula of sample variance and substitute the values.
Σ(xi - x̅)2 / n-1 = 106/5-1
= 106/4
= 26.5
Try the sample variance calculator above to check the accuracy of steps and results.
Example 2: For population variance
Find the population variance of 10, 24, 29, 35, 36, 40.
Solution
You can solve this problem by using the population variance calculator above or manually.
Manually
Below are the steps to solve this problem manually.
Step 1: First of all, calculate the mean of population data.
Mean = µ = Σx/n
= [10 + 24 + 29 + 35 + 36 + 40]/5
= 174/6
= 29
Step 2: Now find the difference between each data value from the mean and the square of the differences.
| Data values (x) | xi - µ | (xi - µ)2 |
| 10 | 10 – 29 = -19 | (-19)2 = 361 |
| 24 | 24 – 29 = -5 | (-5)2 = 25 |
| 29 | 29 – 29 = 0 | (0)2 = 0 |
| 35 | 35 – 29 = 6 | (6)2 = 36 |
| 36 | 36 – 29 = 7 | (7)2 = 49 |
| 40 | 40 – 29 = 11 | (11)2 = 121 |
Step 3: Find the statistical sum of squares.
Σ(xi - µ)2 = 361 + 25 + 0 + 36 + 49 + 121
= 592
Step 4: Take the formula of sample variance and substitute the values.
Σ(xi - µ)2/n = 106/6
= 98.667
Using calculator
Using the population variance calculator above.
Step 1: Select the type of variance.

Step 2: Enter the comma-separated values.

Step 3: Click the calculate button

The result will come in a fraction of a second.

Step-by-step solutions for variance calculations will appear as:

