To calculate result you have to disable your ad blocker first.
Kalkulator wariancji
Aby znaleźć wariancję, wybierz opcję próby lub populacji, wprowadź wartości oddzielone przecinkami i kliknij Oblicz przycisk za pomocą kalkulatora wariancji
Kalkulator wariancji z krokami
Kalkulator wariancji służy do obliczania wariancji próbka I populacja dane. Ten moduł rozwiązywania wariancji znajduje również odchylenie standardowe , mieć na myśli i statystyczną sumę kwadratów jednym kliknięciem.
Co to jest wariancja?
W statystyce przeciętny kwadratów odchyleń od średniej nazywa się zmienność . Decyduje, czy wartości danych są bliższe, czy dalekie od wartości średniej.
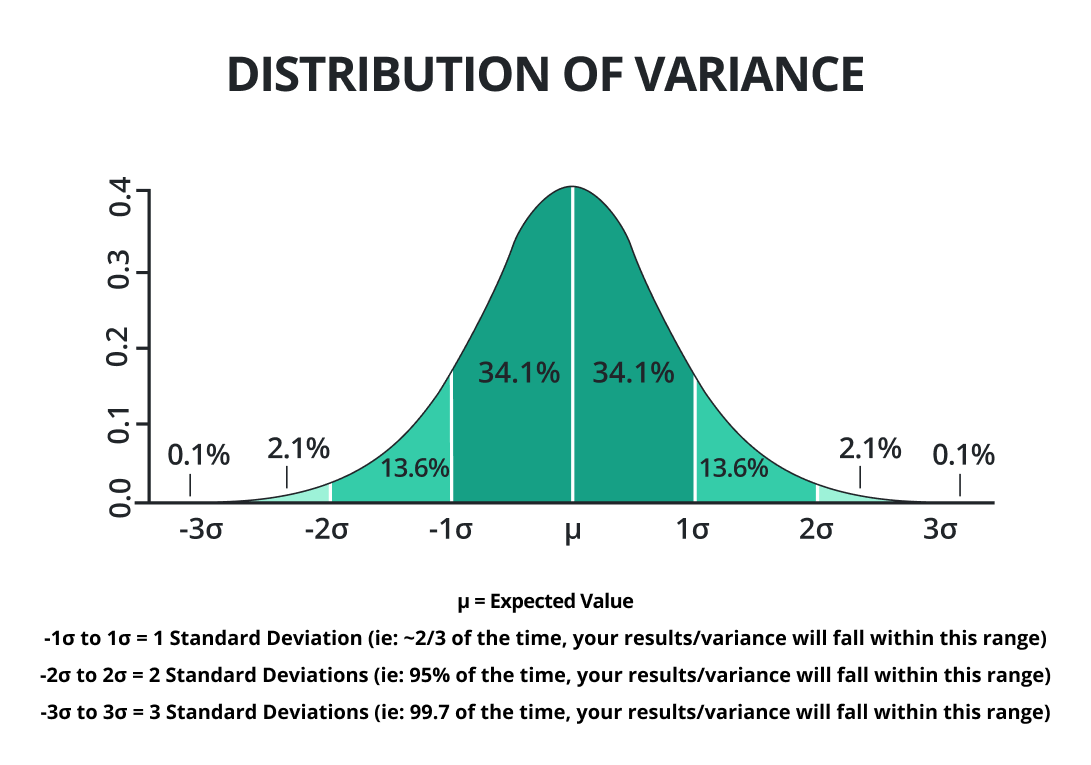
Mała wariancja mówi, że wartości danych losowych są bliższe średniej. Natomiast większa wariancja wskazuje, że wartości danych losowych są dalekie od średniej.
Rodzaje odchyleń
- Przykładowa wariancja
- Wariancja populacji
Formuły wariancyjne
Formuła na Wariancja populacji Jest:
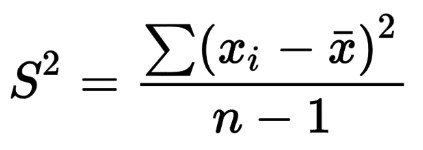
Formuła na wariancja próbki Jest:
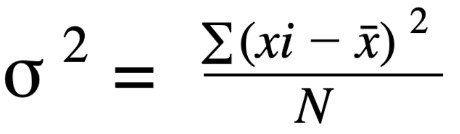
Jak obliczyć wariancję?
Aby dowiedzieć się, jak to zrobić, postępuj zgodnie z poniższymi przykładami obliczyć wariancję .
Przykład 1: Dla wariancji próbki
Znajdź wariancję próbki 12, 14, 15, 19, 25 .
Rozwiązanie
Krok 1: Przede wszystkim, obliczyć średnią przykładowych danych.
Średnia = x̅ = Σx/n
= [12 + 14 + 15 + 19 + 25]/5
= 85/5
= 17
Krok 2: Teraz znajdź różnicę między każdą wartością danych na podstawie średniej i kwadratu różnic.
| Wartości danych (x) | x I - x̅ | (X I - X) 2 |
| 12 | 12 – 17 = -5 | (-5) 2 = 25 |
| 14 | 14 – 17 = -3 | (-3) 2 = 9 |
| 15 | 15 – 17 = -2 | (-2) 2 = 4 |
| 19 | 19 – 17 = 2 | (2) 2 = 4 |
| 25 | 25 – 17 = 8 | (8) 2 = 64 |
Krok 3: Znajdź statystyki suma kwadratów Potem
Σ(x I - X) 2 = 25 + 9 + 4 + 4 + 64
= 106
Krok 4: Weź wzór wariancja próbki i zastąp wartości.
Σ(x I - X) 2 / n-1 = 106/5-1
= 106/4
= 26,5
Wypróbuj powyższy kalkulator wariancji przykładowej, aby sprawdzić dokładność kroków i wyników.
Przykład 2: Dla wariancji populacji
Znajdź wariancję populacji 10, 24, 29, 35, 36, 40 .
Rozwiązanie
Możesz rozwiązać ten problem, korzystając z powyższego kalkulatora wariancji populacji lub ręcznie.
Poniżej znajdują się kroki umożliwiające ręczne rozwiązanie tego problemu.
Krok 1: Przede wszystkim, obliczyć średnią danych populacyjnych.
Średnia = &mikro; = Σx/n
= [10 + 24 + 29 + 35 + 36 + 40]/5
= 174/6
= 29
Krok 2: Teraz znajdź różnicę między każdą wartością danych na podstawie średniej i kwadratu różnic.
| Wartości danych (x) | X I - &mikro; | (X I - &mikro;) 2 |
| 10 | 10 – 29 = -19 | (-19) 2 = 361 |
| 24 | 24 – 29 = -5 | (-5) 2 = 25 |
| 29 | 29 – 29 = 0 | (0) 2 = 0 |
| 35 | 35 – 29 = 6 | (6) 2 = 36 |
| 36 | 36 – 29 = 7 | (7) 2 = 49 |
| 40 | 40 – 29 = 11 | (11) 2 = 121 |
Krok 3: Znaleźć statystyczna suma kwadratów Potem
Σ(x I - &mikro;) 2 = 361 + 25 + 0 + 36 + 49 + 121
= 592
Krok 4: Weź wzór na wariancję próbki i podstaw wartości.
Σ(x I - &mikro;) 2 /n = 106/6
= 98,667

