To calculate result you have to disable your ad blocker first.
Calculadora de varianza
Para encontrar la varianza, seleccione la opción de muestra o población, ingrese los valores separados por comas y haga clic en el botón calcular botón usando la calculadora de varianza
Calculadora de varianza con pasos
La calculadora de varianza se utiliza para encontrar la varianza de muestra y población datos. Este solucionador de varianzas también encuentra la Desviación Estándar , el significar y la suma estadística de cuadrados en un solo clic.
¿Qué es una variación?
En estadística, el promedio de las desviaciones al cuadrado de la media se dice que es la diferencia . Decide si los valores de los datos están más cerca o más lejos del valor promedio.
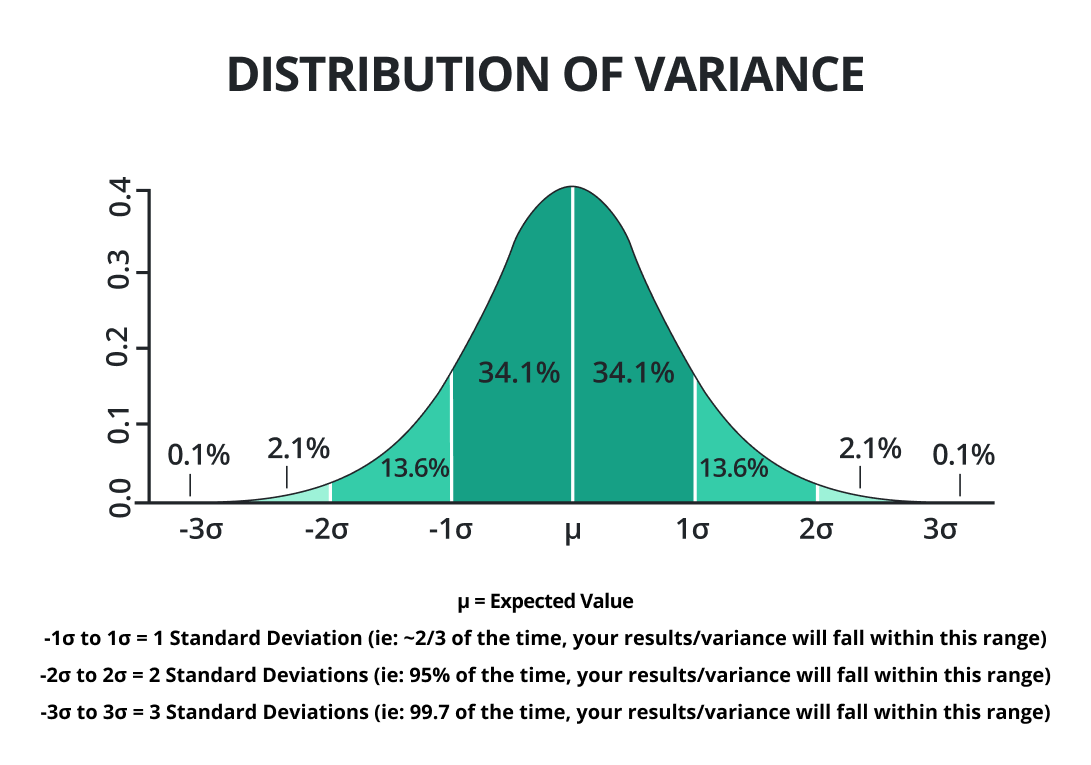
La pequeña varianza indica que los valores de los datos aleatorios están más cerca de la media. Mientras que la mayor varianza indica que los valores de los datos aleatorios están lejos de la media.
Tipos de variaciones
- Variación de la muestra
- Variación de la población
Fórmulas de varianza
La fórmula para el varianza poblacional es:
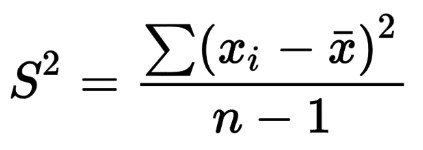
La fórmula para el varianza muestral es:
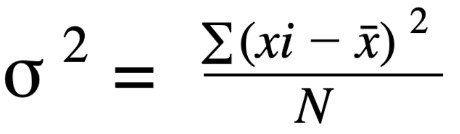
¿Cómo calcular la varianza?
Siga los siguientes ejemplos para aprender cómo calcular la varianza .
Ejemplo 1: para la varianza de la muestra
Encuentre la varianza muestral de 12, 14, 15, 19, 25 .
Solución
Paso 1: En primer lugar, calcular la media de datos de muestra.
Media = x̅ = Σx/n
=[12 + 14 + 15 + 19 + 25]/5
= 85/5
= 17
Paso 2: Ahora encuentre la diferencia entre cada valor de datos de la media y el cuadrado de las diferencias.
| Valores de datos (x) | x i - x̅ | (X i - X) 2 |
| 12 | 12 – ndash; 17 = -5 | (-5) 2 = 25 |
| 14 | 14 – 17 = -3 | (-3) 2 = 9 |
| 15 | 15 – ndash; 17 = -2 | (-2) 2 = 4 |
| 19 | 19 – 17 = 2 | (2) 2 = 4 |
| 25 | 25 – ndash; 17 = 8 | (8) 2 = 64 |
Paso 3: Encuentra la estadística suma de cuadrados .
Σ(x i - X) 2 = 25 + 9 + 4 + 4 + 64
= 106
Etapa 4: Tome la fórmula de varianza muestral y sustituir los valores.
Σ(x i - X) 2 /n-1 = 106/5-1
= 106/4
= 26,5
Pruebe la calculadora de varianza de muestra anterior para verificar la precisión de los pasos y los resultados.
Ejemplo 2: para la varianza de la población
Encuentre la varianza poblacional de 10, 24, 29, 35, 36, 40 Luego luego
Solución
Puedes resolver este problema utilizando la calculadora de varianza de población anterior o manualmente.
A continuación se detallan los pasos para resolver este problema manualmente.
Paso 1: En primer lugar, calcular la media de datos de población.
Media = µ = Σx/n
= [10 + 24 + 29 + 35 + 36 + 40]/5
= 174/6
= 29
Paso 2: Ahora encuentre la diferencia entre cada valor de datos de la media y el cuadrado de las diferencias.
| Valores de datos (x) | X i - µ | (X i -µ) 2 |
| 10 | 10 – 29 = -19 | (-19) 2 = 361 |
| 24 | 24 – 29 = -5 | (-5) 2 = 25 |
| 29 | 29 – 29 = 0 | (0) 2 = 0 |
| 35 | 35 - 29 = 6 | (6) 2 = 36 |
| 36 | 36 – 29 = 7 | (7) 2 = 49 |
| 40 | 40 – ndash; 29 = 11 | (11) 2 = 121 |
Paso 3: Encuentra el suma estadística de cuadrados .
Σ(x i -µ) 2 = 361 + 25 + 0 + 36 + 49 + 121
= 592
Etapa 4: Tome la fórmula de la varianza muestral y sustituya los valores.
Σ(x i -µ) 2 /norte = 106/6
= 98.667

