Chat with us
To calculate result you have to disable your ad blocker first.
차이 계산기
분산을 찾으려면 표본 또는 모집단 옵션을 선택하고 쉼표로 구분된 값을 입력한 후 계산하다 분산 계산기를 사용하는 버튼
Table of Contents:
단계가 포함된 분산 계산기
분산 계산기는 분산을 찾는 데 사용됩니다. 견본 그리고 인구 데이터. 이 분산 솔버는 다음을 찾습니다. 표준 편차 , 평균 , 그리고 한 번의 클릭으로 통계적인 제곱합을 얻을 수 있습니다.
차이란 무엇입니까?
통계에서는 평균 평균으로부터의 편차의 제곱은 다음과 같습니다. 변화 . 데이터 값이 평균 값에 더 가까운지 아니면 먼지를 결정합니다.
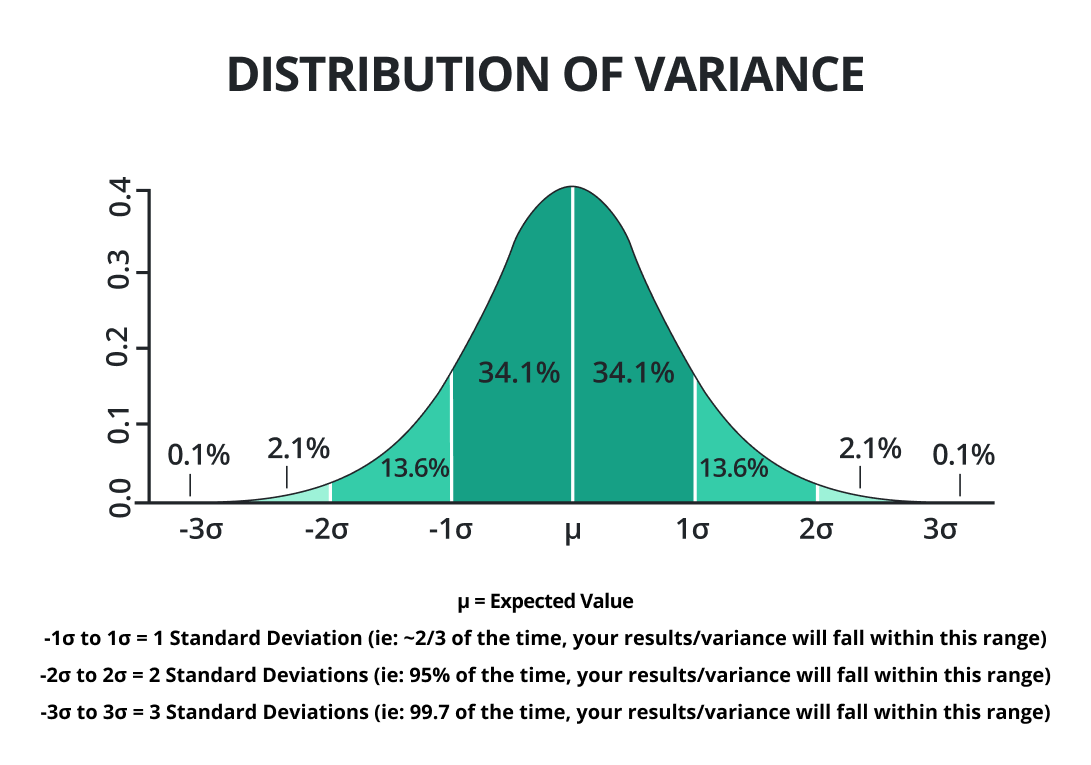
작은 분산은 임의의 데이터 값이 평균에 더 가깝다는 것을 나타냅니다. 분산이 클수록 무작위 데이터 값이 평균에서 멀리 떨어져 있음을 나타냅니다.
분산 유형
- 표본 차이
- 인구 분산
분산의 공식
에 대한 공식 모집단 분산 이다:
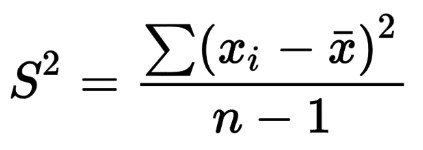
에 대한 공식 표본 분산 이다:
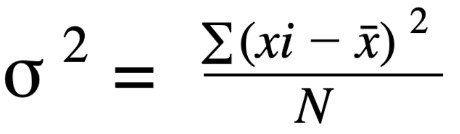
분산을 계산하는 방법은 무엇입니까?
아래 예를 따라 방법을 알아보세요. 분산을 계산하다 .
예 1: 표본 분산의 경우
표본 분산을 구합니다. 12, 14, 15, 19, 25 .
해결책
1 단계: 가장 먼저, 평균을 계산하다 샘플 데이터의
평균 = x̅ = σx/n
= [12 + 14 + 15 + 19 + 25]/5
= 85/5
= 17
2 단계: 이제 평균과 차이의 제곱을 통해 각 데이터 값의 차이를 구합니다.
| 데이터 값 (x) | x 나 - x̅ | (엑스 나 -x̅) 2 |
| 12 | 12 – 17 = -5 | (-5) 2 = 25 |
| 14 | 14 – 17 = -3 | (-삼) 2 = 9 |
| 15 | 15 – 17 = -2 | (-2) 2 = 4 |
| 19 | 19 – 17 = 2 | (2) 2 = 4 |
| 25 | 25 – 17 = 8 | (8) 2 = 64 |
3단계: 통계를 찾아보세요 제곱의 합 .
&시그마;(x 나 -x̅) 2 = 25 + 9 + 4 + 4 + 64
= 106
4단계: 다음의 공식을 취하세요. 표본 분산 값을 대체합니다.
&시그마;(x 나 -x̅) 2 /n-1 = 106/5-1
= 106/4
= 26.5
단계와 결과의 정확성을 확인하려면 위의 샘플 차이 계산기를 사용해 보세요.
예 2: 모집단 분산의 경우
모집단 분산을 구합니다. 10, 24, 29, 35, 36, 40 .
해결책
위의 모집단 분산 계산기를 사용하거나 수동으로 이 문제를 해결할 수 있습니다.
다음은 이 문제를 수동으로 해결하는 단계입니다.
1 단계: 가장 먼저, 평균을 계산하다 인구 데이터의
평균 = Ω = &시그마;x/n
= [10 + 24 + 29 + 35 + 36 + 40]/5
= 174/6
= 29
2 단계: 이제 평균과 차이의 제곱을 통해 각 데이터 값의 차이를 구합니다.
| 데이터 값(x) | 엑스 나 - µ | (엑스 나 - ) 2 |
| 10 | 10 – 29 = -19 | (-19) 2 = 361 |
| 24 | 24 – 29 = -5 | (-5) 2 = 25 |
| 29 | 29 – 29 = 0 | (0) 2 = 0 |
| 35 | 35 – 29 = 6 | (6) 2 = 36 |
| 36 | 36 – 29 = 7 | (7) 2 = 49 |
| 40 | 40 – 29 = 11 | (11) 2 = 121 |
3단계: 찾기 통계적 제곱합 .
&시그마;(x 나 - ) 2 = 361 + 25 + 0 + 36 + 49 + 121
= 592
4단계: 표본 분산의 공식을 취하고 값을 대체합니다.
&시그마;(x 나 - ) 2 /n = 106/6
= 98.667
ADVERTISEMENT
