Калькулятор системы уравнений

калькулятор систем уравнений

Калькулятор системы уравнений — это инструмент, который используется для одновременного решения системы линейных уравнений. Для решения системы линейных уравнений данный калькулятор использует метод замены и метод исключения.

Что такое система уравнений?

А система уравнений представляет собой набор линейных уравнений, которые необходимо решать одновременно. Значения переменных, которые удовлетворяют всем уравнениям системы, будут оцениваться путем решения системы линейных уравнений. 

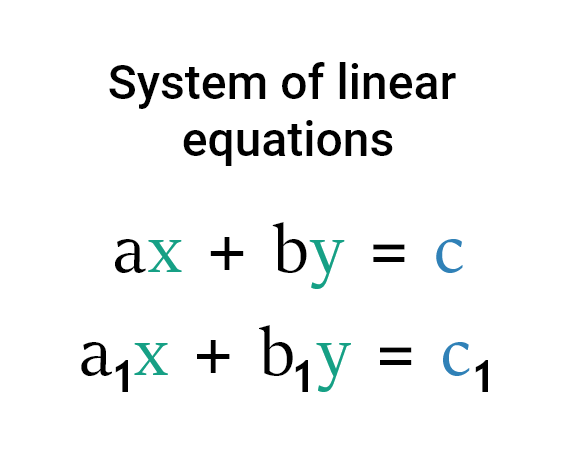
Известны два метода решения системы линейных уравнений.

• Метод устранения
• Метод замены

Что такое метод замещения?

Этот метод используется для решения системы линейных уравнений путем замена значение одной переменной. Найдите значение одной переменной ( скажи “x” ), которая зависит от другой переменной ( скажи «д»; ) по одному уравнению и подставим его в другое уравнение. Чтобы решить систему линейных уравнений путем замены, выполните следующие действия.

• Возьмите одно уравнение из линейной системы и решите его для одного переменная с точки зрения другого.
• Заменять указанное выше значение переменной в других уравнениях и исключите значение переменной с помощью некоторых арифметических операций.
• Решите уравнение сформированный на первом этапе с использованием любого из значений переменных, уже найденных на предыдущих шагах.

Пример метода замены

Решите следующую систему линейных уравнений методом замены.

х + 3у = -4

4х - у = 1

Решение:

Шаг 1: напишите приведенное выше уравнение и дайте название уравнение (я) & уравнение (ii) .

x + 3y = -4 ------> (я)

4x - y = 1 --------> (ii)

Шаг 2: Решите уравнение (я) для “ Икс ”.

х + 3у = -4

х = -4 - 3у

Шаг 3: Замените приведенное выше значение в уравнение (ii) и упростите для « й ”.

Поместите x = -4 -3y в (4x - y = 1)

4(-4 -3г) – у = 1

-16 – 12 лет - у = 1

-16 – 13 лет = 1

– 13 лет = 1 + 16

– 13 лет = 17

  у = 17/(-13)

у = - 17/13

Шаг 4: Поместите указанное выше значение “ й " в шаг 2 и упростить.

y = - 17/13 дюймов (x = -4 -3y)

х = - 4 – 3 (-17/13)

х = - 4 + (51/13)

Решите ее, взяв ЛКМ правой стороны.

х = (-52 + 51)/13

х = -1/13

Следовательно

х = -1/13, у = - 17/13 является решением заданной системы линейных уравнений.

Каков метод устранения?

В этом методе мы устраняем переменную, составляющую тот же коэффициент, с помощью некоторого арифметическая операция (умножить или разделить). Ниже приведены некоторые шаги по устранению значения переменной.

• Возьмите переменные что ты хочешь устранять из уравнения и сделайте коэффициенты переменной одинаковыми.
• Найди ЛКМ выбора переменной путем выбора коэффициентов из всех уравнений.
• Умножить обе части всех уравнений с НОК имеют одинаковые коэффициенты.
• По ситуации добавлять или вычесть уравнение для отмены выбранной переменной.
• Выполнив описанный выше шаг, мы получаем значение одной переменной и используем это значение в любом уравнении, чтобы найти значение исключенной переменной.

Пример метода исключения

Решите следующую систему линейных уравнений методом исключения.

2x – у = 3, х + 2у = 2

Решение:

Шаг 1: Выберите переменную, которую хотите исключить, и запишите приведенное выше уравнение, присвоив ей имя.

2x – у = 3 ------> (я)

х + 2y = 2 ------> (ii)

Устраните “ й ” чтобы получить решение системы простым способом.

Шаг 2: Умножьте на “ 2 ” с уравнение (я) с обеих сторон и получаем.

2(2x – y) = 2(3)

4x - 2y = 6

Шаг 3: Вычтите приведенное выше уравнение с уравнение (ii) и упростить, чтобы исключить “ й ”.

 4x – 2 года = 6

 х + 2у = 2

5х + 0у = 8

Упрощать

5х = 8

х = 8/5 = 1,6

Шаг 4: Поместите указанное выше значение “ Икс ” в уравнение (ii) и упростите, чтобы найти ценность » й ”.

х = 8/5

x + 2y = 2

8/5 + 2у = 2

 2y = 2 – (8/5)

Возьмите LCM с левой стороны.

2y = 2 – (8/5)

2 года = (10 – 8) / 5

2у = (2)/5

у = (2) / (5)(2)

y = 2/10

у = 0,2

Следовательно,

х = 1,6, у = 0,2 является решением заданной системы уравнений.

Часто задаваемые вопросы

Как решить линейные уравнения заменой?

Вот шаги по решению системы линейных уравнений методом замены.

• Определите систему уравнений : Для образования системы должно быть как минимум два линейных уравнения.
• Решите одно уравнение для одной переменной: Одно уравнение должно быть перестановлено, так как слева от уравнения должна быть одна переменная.
• Заменять: Затем подставьте уравнение из предыдущего шага во второе уравнение.
• Упрощать: После замены уравнения из шага 2 все уравнение становится одной переменной и константами, вам придется складывать или вычитать их, чтобы получить результат одной переменной.
• Замените, чтобы найти другую переменную: Подставьте вычисляемую переменную в любое уравнение, чтобы получить результат другой переменной.
• Напишите решение: В конце запишите рассчитанные результаты в упорядоченных парах.

Как решить систему уравнений методом исключения?

Вот шаги по решению системы линейных уравнений методом исключения.

• Прежде всего, запишите данные линейные уравнения в стандартной форме вида Ax + By = C.
• После этого составить коэффициенты напротив любой переменной путем умножения или деления на подходящую цифру.
• Добавьте или вычтите скорректированные уравнения, чтобы исключить одну из переменных. В результате получится уравнение всего с одной переменной.
• Все уравнение становится одной переменной и константами, вам придется складывать или вычитать их, чтобы получить результат одной переменной.
• Затем поместите рассчитанную переменную в любое исходное уравнение, чтобы получить результат другой переменной.

Сколько существует способов решения систем уравнений?

Существует несколько методов решения системы уравнений:

• Метод устранения
• Метод замены
• Правило Крамера
• Матричный метод
• Итеративные методы
• Графический метод

Как графический метод используется для решения системы уравнений?

Вот шаги для решения системы линейных уравнений графическим методом.

1. Прежде всего постройте график первого линейного уравнения.
2. После этого постройте второй график в той же прямоугольной системе координат.
3. Найдите точку пересечения. Также определите, параллельны ли линии или одинаковы.
4. Найдите решение системы линейных уравнений:

• Точка пересечения двух прямых и будет решением системы уравнений.
• Система имеет единственное решение, если прямые пересекаются в одной точке.
• Система не имеет решения, если прямые параллельны и никогда не пересекаются. Это означает, что уравнения несовместны.
• Если две прямые совпадают (являются одной и той же прямой), существует бесконечно много решений. Каждая точка на прямой является решением.