Calculadora De Sistema De Ecuaciones

Calculadora de sistema de ecuaciones

La calculadora de sistemas de ecuaciones es una herramienta que se utiliza para resolver el sistema de ecuaciones lineales simultáneamente. Para resolver el sistema de ecuaciones lineales, esta calculadora utiliza el método de sustitución y el método de eliminación.

¿Qué es un sistema de ecuaciones?

A sistema de ecuaciones es una colección de ecuaciones lineales que deben resolverse simultáneamente. Los valores de las variables que satisfacen todas las ecuaciones del sistema se evaluarían resolviendo un sistema de ecuaciones lineales.

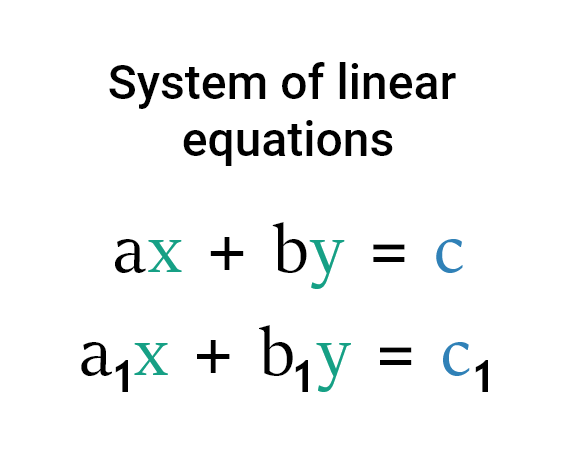
Existen dos métodos bien conocidos para resolver el sistema de ecuaciones lineales.

• Método de eliminación
• Método de sustitución

¿Cuál es el método de sustitución?

Este método se utiliza para resolver un sistema de ecuaciones lineales mediante sustituyendo el valor de una variable. Encuentra el valor de una variable ( diga "x" ) que depende de otra variable ( diga "y" ) por una ecuación y sustitúyela en la otra ecuación. Para resolver el sistema de ecuaciones lineales por sustitución, siga los pasos a continuación.

• Toma una ecuación del sistema lineal y resuélvela para obtener uno. variable en términos de otro.
• Sustituto el valor de la variable anterior en las otras ecuaciones y eliminar el valor de la variable usando algunas operaciones aritméticas.
• Resuelve el ecuación formado en el primer paso utilizando cualquiera de los valores de variable que ya se encuentran en los pasos anteriores.

Ejemplo de método de sustitución

Resuelve el siguiente sistema de ecuaciones lineales por método de sustitución.

x + 3y = -4

4x - y = 1

Solución:

Paso 1: Escribe la ecuación anterior y dale el nombre. ecuación (i) &erio; ecuación (ii) .

x + 3y = -4 ------> (i)

4x - y = 1--------> (ii)

Paso 2: Resuelve el ecuación (i) para " X ".

x + 3y = -4

x = -4 - 3 años

Paso 3: Sustituya el valor anterior en ecuación (ii) y Simplificar para “ y ".

Ponga x = -4 -3y en (4x - y = 1)

4 (-4 -3 años) - ndash; y = 1

-16: 12 años - y = 1

-16: 13 años = 1

- 13 años = 1 + 16

- 13 años = 17

  y = 17/(-13)

y = - 17/13

Etapa 4: Ponga el valor anterior de " y " en paso 2 y simplificar.

y = - 17/13 pulgadas (x = -4 -3y)

x = - 4 – ndash; 3 (-17/13)

x = - 4 + (51/13)

Resuélvelo tomando el LCM del lado derecho.

x = (-52 + 51)/13

x = -1/13

Por eso

x = -1/13, y = - 17/13 es la solución del sistema dado de ecuaciones lineales.

¿Cuál es el método de eliminación?

En este método, eliminamos la variable que tiene el mismo coeficiente por algunos operación aritmética (multiplicar o dividir). A continuación se detallan algunos pasos para eliminar el valor de la variable.

• Toma el variables que quieres eliminar de la ecuación y hacer que los coeficientes de la variable sean iguales.
• Encuentra el LCM de seleccionar una variable eligiendo coeficientes de todas las ecuaciones.
• Multiplicar ambos lados de todas las ecuaciones con el MCM para obtener los mismos coeficientes.
• Según la situación agregar o sustraer la ecuación para cancelar la variable seleccionada.
• Mediante el paso anterior, obtenemos el valor de una variable y usamos este valor en cualquier ecuación para encontrar el valor de la variable eliminada.

Ejemplo de método de eliminación

Resuelve el siguiente sistema de ecuaciones lineales por el método de eliminación.

2x: y = 3, x + 2y = 2

Solución:

Paso 1: Selecciona la variable que quieres eliminar y escribe la ecuación anterior asignándole su nombre.

2x: y = 3------> (i)

x + 2y = 2------> (ii)

Eliminar el “ y " para obtener la solución del sistema de una manera fácil.

Paso 2: Multiplicar por " 2 " con ecuación (i) por ambos lados y conseguimos.

2(2x – y) = 2(3)

4x: 2 años = 6

Paso 3: Resta la ecuación anterior con ecuación (ii) y simplificar para eliminar el “ y ".

 4x: 2 años = 6

 x + 2y = 2

5x + 0y = 8

Simplifique

5x = 8

x = 8/5 = 1,6

Etapa 4: Ponga el valor anterior de " X " en ecuación (ii) y simplifique para encontrar el valor de “ y ".

x = 8/5

x + 2y = 2

8/5 + 2y = 2

 2 años = 2 – (8/5)

Tome el LCM del lado izquierdo.

2y = 2 - (8/5)

2 años = (10 – 8) / 5

2 años = (2) / 5

y = (2) / (5)(2)

y = 2/10

y = 0,2

Por eso,

x = 1.6, y = 0.2 es la solución de un sistema de ecuaciones dado.

Preguntas frecuentes

¿Cómo resolver ecuaciones lineales por sustitución?

A continuación se detallan los pasos para resolver un sistema de ecuaciones lineales mediante el método de sustitución.

• Identificar el sistema de ecuaciones. : Debe haber al menos dos ecuaciones lineales para formar un sistema.
• Resuelva una ecuación para una variable: Se debe reorganizar una ecuación, ya que debería haber una variable a la izquierda de la ecuación.
• Sustituto: Luego sustituya la ecuación del paso anterior por la segunda ecuación.
• Simplificar: Después de sustituir, la ecuación del paso 2, toda la ecuación se convierte en una variable y constantes, debes sumarlas o restarlas para obtener el resultado de una variable.
• Sustituir para encontrar la otra variable: Sustituye la variable calculada en cualquier ecuación para obtener el resultado de la otra variable.
• Escribe la solución: Al final, escribe los resultados calculados en pares ordenados.

¿Cómo resolvemos un sistema de ecuaciones por eliminación?

A continuación se detallan los pasos para resolver un sistema de ecuaciones lineales mediante el método de eliminación.

• En primer lugar, escribe las ecuaciones lineales dadas en forma estándar como Ax + By = C.
• Después de eso, haz los coeficientes opuestos a cualquier variable multiplicando o dividiendo por un dígito adecuado.
• Suma o resta las ecuaciones ajustadas para eliminar una de las variables. Esto dará como resultado una ecuación con una sola variable.
• Toda la ecuación se convierte en una variable y constantes, hay que sumarlas o restarlas para obtener el resultado de una variable.
• Luego, coloque la variable calculada en cualquier ecuación original para obtener el resultado de la otra variable.

¿Cuántos métodos existen para resolver sistemas de ecuaciones?

Existen varios métodos para resolver un sistema de ecuaciones:

• Método de eliminación
• Método de sustitución
• La regla de Cramer
• Método matricial
• Métodos iterativos
• Método gráfico

¿Cómo se utiliza el método de gráficas para resolver un sistema de ecuaciones?

Estos son los pasos para resolver un sistema de ecuaciones lineales mediante el método gráfico.

1. En primer lugar, traza la gráfica de la primera ecuación lineal.
2. Después de eso, traza el segundo gráfico en el mismo sistema de coordenadas rectangular.
3. Encuentra el punto de intersección. Además, determine si las líneas son paralelas o las mismas.
4. Encuentra la solución de un sistema de ecuaciones lineales:

• El punto donde se cruzan dos rectas será la solución del sistema de ecuaciones.
• El sistema tiene una única solución si las rectas se cruzan en un punto.
• El sistema no tiene solución si las rectas son paralelas y nunca se cruzan. Esto significa que las ecuaciones son inconsistentes.
• Si las dos rectas coinciden (son la misma recta), existen infinitas soluciones. Cada punto de la recta es una solución.