連立方程式計算機

連立方程式計算機

連立方程式計算機は、連立一次方程式を同時に解くために使用されるツールです。連立一次方程式を解くために、この計算機は代入法と消去法を使用します。

連立方程式とは何ですか?

あ 方程式系 は、同時に解く必要がある一次方程式の集合です。システム内のすべての方程式を満たす変数の値は、連立一次方程式を解くことによって評価されます。

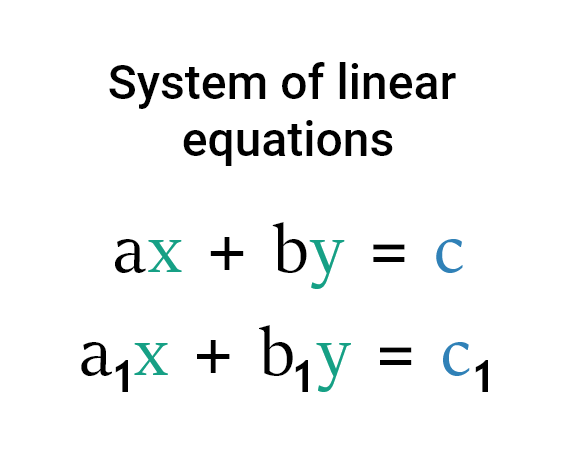
連立一次方程式を解くには 2 つのよく知られた方法があります。

• 消去法
• 置換方法

置換方法とは何ですか?

この方法は、次のようにして連立一次方程式を解くために使用されます。 代替 1 つの変数の値。 1 つの変数の値を見つけます ( 「×」と言います。 ) 別の変数 ( 「y」と言います。 ) を 1 つの式で計算し、それを他の式に代入します。代入によって連立一次方程式を解くには、以下の手順に従います。

• 線形システムから 1 つの方程式を取り出し、それを 1 つの方程式について解きます。 変数 別の観点から言えば。
• 代わりの 上記の変数値を他の式に組み込み、算術演算を使用して変数の値を削除します。
• を解決します。 方程式 上記のステップですでに見つかった変数値のいずれかを使用して、最初のステップで形成されます。

置換方法の例

次の連立一次方程式を代入法で解きます。

x + 3y = -4

4x - y = 1

解決：

ステップ1： 上式を書いて名前を付けます 式(i) & 式(ii) 。

x + 3y = -4 ------> （私）

4x - y = 1--------> (ii)

ステップ2： を解決します。 式(i) 「」の場合 バツ ”。

x + 3y = -4

x = -4 - 3y

ステップ 3: 上記の値をに代入します。 式(ii) “ については簡素化します。 y ”。

(4x - y = 1) に x = -4 -3y を代入します。

4(-4 -3y) – y = 1

-16 – 12y - y = 1

-16 – 13y = 1

– 13y = 1 + 16

– 13y = 17

  y = 17/(-13)

y = - 17/13

ステップ 4: 上記の値 “ を入力します。 y " で ステップ2 そして簡素化します。

y = - 17/13 インチ (x = -4 -3y)

x = - 4 – 3 (-17/13)

x = - 4 + (51/13)

を取ることでそれを解決します LCM 右側の。

x = (-52 + 51)/13

x = -1 / 13

したがって、

x = -1 / 13、y = - 17/13 は、指定された線形方程式系の解です。

消去法とは何ですか？

この方法では、同じ係数を作る変数をいくつかの方法で削除します。 四則演算 (乗算または除算)。変数の値を削除するためのいくつかの手順を以下に示します。

• 取ってください 変数 あなたがしたいこと なくす 方程式から変数の係数を同じにします。
• を見つける LCM すべての方程式から係数を選択して変数を選択する方法。
• かける LCM を使用してすべての方程式の両辺を計算し、同じ係数を作成します。
• 状況に応じて 追加 または 引き算 選択した変数をキャンセルするための式。
• 上記のステップでは、1つの変数の値を取得し、任意の方程式でこの値を使用して、排除された変数の値を見つけます。

消去法の例

排除法により、次の線形方程式のシステムを解きます。

2倍y = 3、x + 2y = 2

解決：

ステップ1： 削除したい変数を選択し、名前を付けて上記の式を記述します。

2倍y = 3-----> （私）

x + 2y = 2-----> (ii)

「」を削除します。 y ”簡単な方法でシステムの解決策を取得します。

ステップ2： “ を掛けます。 2 ”と 式(i) 両側で、そして私たちは得ます。

2(2x – y) = 2(3)

4x – 2y = 6

ステップ 3: 上式を次のように引き算します。 式(ii) “ を削除して簡素化します。 y ”。

 4x – 2y = 6

 x + 2y = 2

5x + 0y = 8

簡素化 

5x = 8

x = 8/5 = 1.6

ステップ 4: 上記の値 “ を入力します。 バツ ”で 方程式（ii） “ の値を見つけるのが簡単になります。 y ”。

x = 8/5

x + 2y = 2

8/5 + 2y = 2

 2y = 2 – (8/5)

左側の最小公倍数を取ります。

2y = 2 – (8/5)

2y = (10 – 8) / 5

2y = (2) / 5

y = (2) / (5)(2)

y = 2/10

y = 0.2

したがって、

x = 1.6、y = 0.2 は、指定された連立方程式の解です。

よくある質問

置換によって線形方程式を解く方法は？

ここでは、代入法によって連立一次方程式を解く手順を示します。

• 方程式系を特定する : システムを形成するには、少なくとも 2 つの線形方程式が必要です。
• 1 つの変数に対して 1 つの方程式を解く： 方程式の左側には変数が 1 つあるはずなので、1 つの方程式を再配置する必要があります。
• 代わりの： 次に、上のステップの式を 2 番目の式に代入します。
• 簡略化する： ステップ 2 の式を代入すると、式全体が 1 つの変数と定数になります。1 つの変数の結果を得るには、それらを加算または減算する必要があります。
• 他の変数を見つけるために代入します。 計算された変数を式に代入して、他の変数の結果を取得します。
• 解決策を書きます: 最後に、計算結果を順序付きペアで書き込みます。

連立方程式を消去法で解くにはどうすればよいでしょうか?

ここでは、消去法によって連立一次方程式を解く手順を示します。

• まず第一に、ax + by = Cのような標準形式の指定された線形方程式を書きます。
• その後、適切な桁で乗算または除算して、任意の変数の逆の係数を作成します。
• 調整された方程式を加算または減算して、変数の 1 つを除去します。これにより、変数が 1 つだけの方程式が作成されます。
• 方程式全体が 1 つの変数と定数になるため、1 つの変数の結果を得るにはそれらを加算または減算する必要があります。
• 次に、計算された変数を元の方程式に代入して、他の変数の結果を取得します。

連立方程式を解く方法は何通りありますか?

連立方程式を解く方法はいくつかあります。

• 消去法
• 置換方法
• クレイマーの法則
• マトリックス法
• 反復法
• グラフ化方法

グラフ作成法は連立方程式を解くためにどのように使用されますか?

ここでは、グラフ法を使用して連立一次方程式を解く手順を示します。

1. まず、最初の一次方程式のグラフをプロットします。
2. その後、2 番目のグラフを同じ直交座標系にプロットします。
3. 交点を見つけます。また、線が平行か同一かを判断します。
4. 連立一次方程式の解を求める：

• 2 本の直線が交差する点が連立方程式の解になります。
• 線が 1 点で交差する場合、システムには 1 つの固有の解決策があります。
• 線が平行で決して交わらない場合、システムには解決策がありません。これは方程式が矛盾していることを意味します。
• 2 つの直線が一致する (同じ直線である) 場合、解は無限に存在します。線上のすべての点が解決策です。