Gleichungssystem-Rechner

Gleichungssystem-Rechner

Der Gleichungssystemrechner ist ein Werkzeug, mit dem das System linearer Gleichungen gleichzeitig gelöst werden kann. Um das System linearer Gleichungen zu lösen, verwendet dieser Rechner die Substitutionsmethode und die Eliminationsmethode.

Was ist ein Gleichungssystem?

A Gleichungssystem ist eine Sammlung linearer Gleichungen, die gleichzeitig gelöst werden sollen. Die Werte der Variablen, die alle Gleichungen im System erfüllen, würden durch Lösen eines Systems linearer Gleichungen ausgewertet.

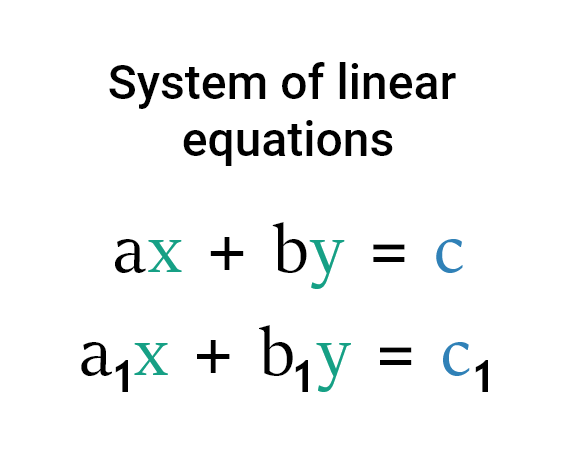
Es gibt zwei bekannte Methoden zur Lösung des Systems linearer Gleichungen.

• Eliminierungsmethode
• Substitutionsmethode

Was ist die Substitutionsmethode?

Mit dieser Methode wird ein System linearer Gleichungen gelöst ersetzen der Wert einer Variablen. Finden Sie den Wert einer Variablen ( Sagen Sie „x“ ), die von einer anderen Variablen abhängt ( Sagen Sie „J“ ) durch eine Gleichung und setze sie in die andere Gleichung ein. Um das lineare Gleichungssystem durch Substitution zu lösen, befolgen Sie die folgenden Schritte.

• Nehmen Sie eine Gleichung aus dem linearen System und lösen Sie sie nach einer Variable in einem anderen.
• Ersatz Der obige variable Wert in den anderen Gleichungen und eliminiert den Wert der Variablen mit einigen arithmetischen Operationen.
• Löse das Gleichung wird im ersten Schritt unter Verwendung beliebiger Variablenwerte gebildet, die bereits in den obigen Schritten gefunden wurden.

Beispiel einer Substitutionsmethode

Lösen Sie das folgende lineare Gleichungssystem mit der Substitutionsmethode.

x + 3y = -4

4x - y = 1

Lösung:

Schritt 1: Schreiben Sie die obige Gleichung und geben Sie den Namen an Gleichung (i) & Gleichung (ii) Dann dann

x + 3y = -4 ------> (ich)

4x - y = 1--------> (ii)

Schritt 2: Löse das Gleichung (i) für „ X “.

x + 3y = -4

x = -4 - 3y

Schritt 3: Ersetzen Sie den oben genannten Wert durch Gleichung (ii) und vereinfachen Sie “ j “.

Setzen Sie x = -4 -3y in (4x - y = 1)

4 (-4 -3y) -y = 1

-16 – 12y - y = 1

-16 – 13y = 1

– 13y = 1 + 16

– 13 Jahre = 17

  y = 17/(-13)

y = - 17/13

Schritt 4: Setzen Sie den obigen Wert von “ j " In Schritt 2 und vereinfachen.

y = - 17/13 Zoll (x = -4 -3y)

x = - 4 – 3 (-17/13)

x = - 4 + (51/13)

Lösen Sie es, indem Sie das nehmen LCM der rechten Seite.

x = (-52 + 51)/13

x = -1 / 13

Somit

x = -1 / 13, y = - 17/13 ist die Lösung des gegebenen Systems der linearen Gleichungen.

Was ist die Eliminierungsmethode?

Bei dieser Methode eliminieren wir die Variable, die den gleichen Koeffizienten für einige erzeugt Arithmetische Operation (multiplizieren oder dividieren). Im Folgenden werden einige Schritte zum Eliminieren des Werts der Variablen aufgeführt.

• Nehmen Sie die Variablen dass du willst beseitigen aus der Gleichung und machen Sie die Koeffizienten der Variablen gleich.
• Finden Sie die LCM der Auswahl einer Variablen durch Auswahl von Koeffizienten aus allen Gleichungen.
• Multiplizieren beide Seiten aller Gleichungen mit dem LCM, um die gleichen Koeffizienten zu erhalten.
• Je nach Situation hinzufügen oder subtrahieren die Gleichung, um die ausgewählte Variable zu löschen.
• Durch den obigen Schritt erhalten wir den Wert einer Variablen und verwenden diesen Wert in einer beliebigen Gleichung, um den Wert der eliminierten Variablen zu ermitteln.

Beispiel einer Eliminierungsmethode

Lösen Sie das folgende lineare Gleichungssystem mit der Eliminierungsmethode.

2x – y = 3, x + 2y = 2

Lösung:

Schritt 1: Wählen Sie die Variable aus, die Sie eliminieren möchten, und schreiben Sie die obige Gleichung, indem Sie ihren Namen zuweisen.

2x – y = 3------> (ich)

x + 2y = 2------> (ii)

Beseitigen Sie das „ j “ um auf einfache Weise die Lösung des Systems zu erhalten.

Schritt 2: Mit “ multiplizieren 2 “ mit Gleichung (i) auf beiden Seiten und wir bekommen.

2(2x – y) = 2(3)

4x – 2y = 6

Schritt 3: Subtrahieren Sie die obige Gleichung mit Gleichung (ii) und vereinfachen, um die „ j “.

 4x – 2y = 6

 x + 2y = 2

5x + 0y = 8

Vereinfachen Sie

5x = 8

x = 8/5 = 1,6

Schritt 4: Geben Sie den oben genannten Wert von “ X “ In Gleichung (ii) und vereinfachen, um den Wert von “ j “.

x = 8/5

x + 2y = 2

8/5 + 2y = 2

 2y = 2 – (8/5)

Nehmen Sie das LCM der linken Seite.

2y = 2 – (8/5)

2y = (10 – 8) / 5

2y = (2) / 5

y = (2) / (5)(2)

y = 2/10

y = 0,2

Somit,

x = 1,6, y = 0,2 ist die Lösung eines gegebenen Gleichungssystems.

FAQs

Wie löst man lineare Gleichungen durch Substitution?

Hier sind die Schritte zum Lösen eines Systems linearer Gleichungen durch die Substitutionsmethode.

• Identifizieren Sie das Gleichungssystem : Es sollten mindestens zwei lineare Gleichungen vorhanden sein, um ein System zu bilden.
• Lösen Sie eine Gleichung für eine Variable: Eine Gleichung sollte neu angeordnet werden, da sich links von der Gleichung eine Variable befinden sollte.
• Ersatz: Ersetzen Sie dann die Gleichung aus dem obigen Schritt durch die zweite Gleichung.
• Vereinfachen: Nach dem Ersetzen der Gleichung aus Schritt 2 wird die gesamte Gleichung zu einer Variablen und Konstanten. Sie müssen diese addieren oder subtrahieren, um das Ergebnis einer Variablen zu erhalten.
• Ersetzen Sie, um die andere Variable zu finden: Ersetzen Sie die berechnete Variable durch eine beliebige Gleichung, um das Ergebnis der anderen Variablen zu erhalten.
• Schreiben Sie die Lösung: Schreiben Sie am Ende die berechneten Ergebnisse in geordnete Paare.

Wie löst man ein Gleichungssystem durch Eliminierung?

Hier sind die Schritte zum Lösen eines Systems linearer Gleichungen durch die Eliminationsmethode.

• Schreiben Sie zunächst die gegebenen linearen Gleichungen in Standardform wie Ax + By = C.
• Machen Sie anschließend die Koeffizienten einer beliebigen Variablen entgegengesetzt, indem Sie sie mit einer geeigneten Ziffer multiplizieren oder dividieren.
• Addieren oder subtrahieren Sie die angepassten Gleichungen, um eine der Variablen zu eliminieren. Dies führt zu einer Gleichung mit nur einer Variablen.
• Die gesamte Gleichung wird zu einer Variablen und Konstanten. Sie müssen diese addieren oder subtrahieren, um das Ergebnis einer Variablen zu erhalten.
• Setzen Sie dann die berechnete Variable in eine beliebige Originalgleichung ein, um das Ergebnis der anderen Variablen zu erhalten.

Wie viele Methoden gibt es, Gleichungssysteme zu lösen?

Es gibt mehrere Methoden, ein Gleichungssystem zu lösen:

• Eliminierungsmethode
• Substitutionsmethode
• Cramers Regel
• Matrix-Methode
• Iterative Methoden
• Grafikmethode

Wie wird die grafische Methode zur Lösung eines Gleichungssystems verwendet?

Hier sind die Schritte zum Lösen eines Systems linearer Gleichungen mithilfe der grafischen Methode.

1. Zeichnen Sie zunächst den Graphen der ersten linearen Gleichung.
2. Zeichnen Sie anschließend den zweiten Graphen auf demselben rechteckigen Koordinatensystem.
3. Finden Sie den Schnittpunkt. Bestimmen Sie außerdem, ob die Linien parallel oder gleich sind.
4. Finden Sie die Lösung eines linearen Gleichungssystems:

• Der Punkt, an dem sich zwei Geraden schneiden, ist die Lösung des Gleichungssystems.
• Das System hat eine eindeutige Lösung, wenn sich die Linien in einem Punkt schneiden.
• Das System hat keine Lösung, wenn die Geraden parallel sind und sich nie schneiden. Das bedeutet, dass die Gleichungen inkonsistent sind.
• Wenn die beiden Geraden zusammenfallen (die gleiche Gerade sind), gibt es unendlich viele Lösungen. Jeder Punkt auf der Linie ist eine Lösung.