Калькулятор квадратных корней

калькулятор квадратный корень

калькулятор квадратный корень устраняет необходимость делить числа для нахождения корней. Найдите как совершенные, так и несовершенные квадратные корни с помощью упростителя квадратного корня.

Что такое корень квадратный?

Квадратный корень из числа А находит число Б, которое при умножении само на себя снова дает число А. В математической форме:

√x = y, где y * y = x 

Существуют и другие способы вычислить квадратный корень. Его можно определить как дробь, а показатель степени можно сформировать как:

Х  ^1/2 = Y, где Y ² = Х

Квадратный корень числа дает два значения: точное число, но противоположные знаки. Например, квадратный корень из 4 является +2 и -2 . +2 называется главным квадратным корнем. 

Если число — это площадь квадрата, то его квадратный корень даст величину его одной стороны. Аналогично, обратный расчет дает площадь квадрата.  

Есть два типа квадратных корней; совершенный и несовершенный. Идеальный квадратный корень — это значение, которое принимает целое число, например &радик;16 = 4 в то время как примером несовершенного квадратного корня будет &радик;15 = 3,87 .

Как найти квадратный корень?

Научные калькуляторы обычно имеют кнопку квадратного корня. Но если у вас нет доступа к калькулятору, вы всегда можете воспользоваться онлайн-Калькулятор квадратных корней.

Квадратный корень можно вычислить вручную, но этот метод требует много времени. Четыре способа найти квадратный корень числа:

• Метод вычитания
• Длинное деление
• Метод проб и ошибок
• Метод простой факторизации

Метод вычитания

В первом методе из значения последовательно вычитаются нечетные числа до тех пор, пока 0 останки. Количество раз, которое будет выполнено вычитание, будет равно квадратному корню. Это применимо только к идеальным квадратам. 

Пример:

Решать 25 используя этот метод, сначала вычтите 1 от него.

25 - 1 = 24
24-3 = 21
21 – 5 = 16
16 - 7 = 9
9 - 9 = 0

Общее количество выполненных вычитаний равно 5 и это квадратный корень. 

Длинный дивизион

Второй метод – это длинное подразделение . Оно немного отличается от обычного деления. Начните с деления на максимально возможную цифру. На следующем шаге прибавьте этот радикальный коэффициент к самому себе и поместите рядом с ним значение частного. 

Если радикальный коэффициент состоит из двух цифр, то прибавляем цифру с меньшим разрядом. 

Разделите, используя это новое число, и повторяйте, пока не получите ноль или пока деление станет невозможным.

Пример:

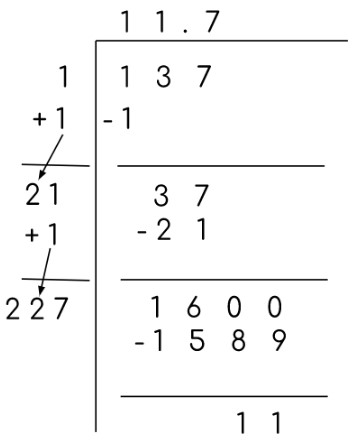
Этот является примером несовершенного квадрата, который также доказывает, что этот метод может решить несовершенные квадраты.

Метод проб и ошибок

Третий метод называется методом проб и ошибок. Он используется во многих математических расчетах, но его часто пропускают, поскольку он занимает много времени. Кроме того, вам нужно выучить идеальные квадраты, чтобы использовать это.

По сути, вам нужно угадать значение. Вы видите, между какими двумя идеальными квадратными корнями оно лежит. Нравиться 10 между 9 и 16 . Таким образом, его квадратный корень должен находиться где-то между 3 и 4 . 

Затем вы замечаете, какое значение находится рядом. В нашем примере 10 ближе к 9 чем 16 . Итак, это может быть 3.1 или 3.2 . Возьмите квадрат и проверьте. 

Площадь 3.1 является 9,61 и что из 3.2 является 10.24 . Большей точности можно добиться, угадав следующий десятичный знак. скажем так 3.15 или 3.16 или 3.17 . Возведя в квадрат все три, мы получим:
9,9225, 9,9856 и 10,0487. . Давайте попробуем найти еще раз. Как насчет 3.162 и 3 .163 . Их квадраты 9,998244 и 10.004567 . Оба очень близки 10 .  

Простые множители

Четвертый и последний метод называется факторизацией простых чисел, поскольку множители числа вычисляются для получения его квадратного корня. Он также используется только для идеальных квадратов. 

Факторы выбираются попарно и решаются.

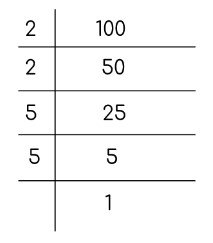
= 2 х 2 х 5 х 5
= 2 ² х 5 ²
= (2 х 5) ²
= (10) ²

Таким образом, квадратный корень из 100 равен 10.