平方根計算機

平方根計算 

平方根計算機を使用すると、ルートを見つけるために数字を割る手間が不要になります。平方根簡略化機能を使用して、完全平方根と不完全平方根の両方を求めます。

平方根とは何ですか?

数値 A の平方根は数値 B を求め、それを再度乗算すると数値 A が得られます。数学的形式では:

                                  √X = Y ここで、Y * Y = X 

平方根を定義する他の方法もあります。で定義できます 分数 そして 指数 次のような形式になります:

                                   X ^1/2 = Y ここで Y ² = X

数値の平方根は 2 つの値を与えます: 正確な数値ですが、符号は反対です。たとえば、次の平方根は 4 は +2 そして -2 。の +2 は主平方根と呼ばれます。

数値が正方形の面積である場合、その平方根はその一辺の寸法を示します。同様に、逆算して正方形の面積を求めます。  

平方根には 2 つのタイプがあります。完璧と不完全。完全平方根は、次のような整数に解決される値です。 √16 = 4 一方、不完全な平方根の例は次のとおりです。 √15 = 3.87 。

平方根を見つけるにはどうすればよいですか?

通常、関数電卓には開平演算ボタンが付いています。ただし、電卓にアクセスできない場合は、いつでもオンライン平方根単純化ツールを使用できます。

平方根を手動で計算することも可能ですが、その方法には時間がかかります。数値の平方根を求める 4 つの方法は次のとおりです。

• 減算法
• 長い分割
• 試行錯誤の方法
• 素因数分解法

減算法

最初の方法では、値から奇数を順番に減算し、 0 残っています。減算した回数が平方根となります。これは完全正方形にのみ適用されます。 

例：

解決するには 25 この方法を使用すると、まず減算します 1 それから。

25 - 1 = 24
24 - 3 = 21
21 - 5 = 16
16 - 7 = 9
9 - 9 = 0

行われた減算の合計数は次のとおりです。 5 これが平方根です。 

長い部門

2番目の方法は、 長い分割 。通常の部門とは少し異なります。まずは可能な最大の桁で割ります。次のステップでは、その根号係数をそれ自体に加算し、その隣に商の値を置きます。

部首係数が 2 桁の場合は、小さい方の位の値にその桁を加算します。

この新しい数値を使用して除算を繰り返し、ゼロになるか、それ以上除算ができなくなるまで繰り返します。

例：

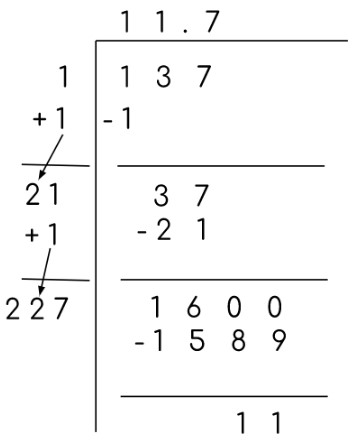
これは不完全平方の例であり、この方法で不完全平方を解決できることも証明しています。

試行錯誤の方法

3 番目の方法は、トライアンドエラー法と呼ばれます。多くの数学的計算で使用されますが、時間がかかるためスキップされることがよくあります。また、これを使用するには完全平方を学習する必要があります。

基本的に、値を推測する必要があります。 2 つの完全平方根の間にあることがわかります。のように 10 は間に 9 そして 16 。したがって、その平方根は次の間のどこかにある必要があります。 3 そして 4 . 

次に、どの値が近いかがわかります。私たちの例では、 10 に近いです 9 よりも 16 。だから、そうかもしれない 3.1 または 3.2 。四角形を取って確認してください。 

の正方形 3.1 は 9.61 そしてそれの 3.2 は 10.24 。次の小数点以下の桁を推測すると、さらに正確になります。そうだとしましょう 3.15 または 3.16 または 3.17 。 3 つすべてを 2 乗すると、次のようになります。
9.9225、9.9856、10.0487 。もう一度探してみましょう。どうですか 3.162 そして3 .163 。彼らの正方形は、 9.998244 そして 10.004567 。どちらも非常に近いです 10 。  

素因数分解

4 番目で最後の方法は、数値の因数を計算して平方根を求めるため、素因数分解と呼ばれます。また、完全正方形のみに使用されます。

因子はペアで選択され、解決されます。

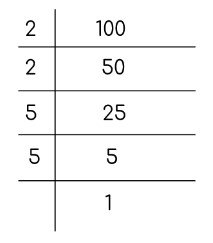
= 2 × 2 × 5 × 5
= 2 ² ×5 ²
= (2 x 5) ²
= (10) ²

したがって、100 の平方根は 10 です。