Calculadora de raiz quadrada

Calculadora de raiz quadrada

A calculadora de raiz quadrada elimina o esforço de divisão de dígitos para encontrar as raízes. Encontre raízes quadradas perfeitas e imperfeitas usando o simplificador de raiz quadrada.

O que é raiz quadrada?

A raiz quadrada de um número A encontra um número B que, ao multiplicar por si só, novamente fornece o número A. em forma matemática:

                                  √X = Y onde Y * Y = X 

Existem outras maneiras de definir a raiz quadrada também. Pode ser definido em fração e expoente forma como:

                                  X ^1/2 = S onde Y ² = X

A raiz quadrada de um número fornece dois valores: o número exato, mas sinais opostos. Por exemplo, a raiz quadrada de 4 é +2 e -2 . O +2 é chamado de raiz quadrada principal.

Se um número é a área de um quadrado, então sua raiz quadrada dará a medida de seu lado. Da mesma forma, o cálculo regressivo fornece a área do quadrado.  

Existem dois tipos de raízes quadradas; perfeito e imperfeito. A raiz quadrada perfeita é um valor que resolve um número inteiro como √16 = 4 enquanto um exemplo de raiz quadrada imperfeita será √15 = 3,87 Então então

Como encontrar a raiz quadrada?

Normalmente, as calculadoras científicas vêm com o botão de operação de raiz quadrada. Mas se você não tiver acesso a uma calculadora, poderá usar o simplificador online de raiz quadrada.

É possível calcular a raiz quadrada manualmente, mas os métodos são demorados. As quatro maneiras de encontrar a raiz quadrada de um número são:

• Método de subtração
• Divisão longa
• Método de tentativa e erro
• Método de fatoração principal

Método de subtração

No primeiro método, subtraia os números ímpares em sequência do valor até 0 restos. O número de vezes que a subtração é feita será a raiz quadrada. Só é aplicável a quadrados perfeitos.

Exemplo:

Resolver 25 usando este método, primeiro, subtraia 1 a partir dele.

25-1 = 24
24 - 3 = 21
21 - 5 = 16
16 - 7 = 9
9 - 9 = 0

O número total de subtrações feitas é 5 e esta é a raiz quadrada.

Divisão longa

O segundo método é o divisão longa . É um pouco diferente da divisão habitual. Comece dividindo pelo maior dígito possível. Para a próxima etapa, adicione esse coeficiente radical a si mesmo e coloque o valor do quociente próximo a ele.

Se o coeficiente de radical consistir em dois dígitos, adicione o dígito no menor valor do local.

Divida usando este novo número e repita até obter zero ou não for possível mais divisão.

Exemplo:

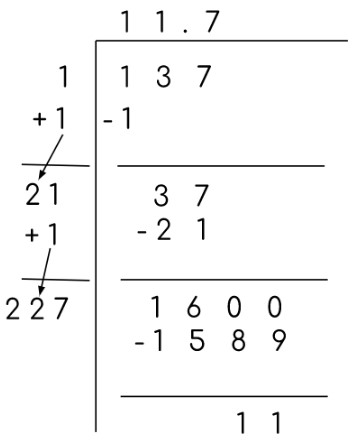
Este é um exemplo de quadrado imperfeito que também prova que este método pode resolver quadrados imperfeitos.

Método de tentativa e erro

O terceiro método é chamado de método de tentativa e erro. É usado em muitos cálculos matemáticos, mas muitas vezes é ignorado porque leva muito tempo. Além disso, você precisa aprender os quadrados perfeitos para usar isso.

Basicamente, você tem que adivinhar o valor. Você vê entre as duas raízes quadradas perfeitas. Como 10 está entre 9 e 16 . Portanto, sua raiz quadrada deve estar em algum lugar entre 3 e 4 . 

Então você percebe qual valor está próximo. Em nosso exemplo, 10 está mais perto de 9 que 16 . Então, pode ser 3.1 ou 3.2 . Pegue o quadrado e confira.

A praça de 3.1 é 9,61 e aquele de 3.2 é 10.24 . Mais precisão pode ser alcançada adivinhando a próxima casa decimal. Digamos que é 3.15 ou 3.16 ou 3.17 . Tomando quadrados de todos os três, temos:
9.9225, 9.9856 e 10.0487 . Vamos tentar encontrar mais uma vez. A respeito 3.162 e 3 .163 . Seus quadrados são 9.998244 e 10.004567 . Ambos estão muito próximos 10 .  

Fatoração Primária

O quarto e último método é chamado de fatoração primária porque os fatores do número são calculados para obter sua raiz quadrada. Também é usado apenas para quadrados perfeitos.

Os fatores são selecionados em pares e resolvidos.

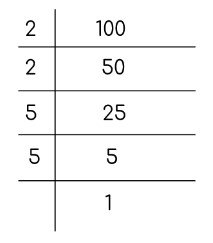
= 2x2x5x5
= 2 ² x 5 ²
= (2x5) ²
= (10) ²

Portanto, a raiz quadrada de 100 é 10.