To calculate result you have to disable your ad blocker first.
Raíz Cuadrada Calculadora
Para usar la calculadora de raíz cuadrada, ingrese el número y haga clic en calcular.
Calculadora de raíz cuadrada
La calculadora de raíces cuadradas elimina el esfuerzo de dividir dígitos para encontrar las raíces. Encuentre raíces cuadradas perfectas e imperfectas usando el simplificador de raíces cuadradas.
¿Qué es la raíz cuadrada?
La raíz cuadrada de un número A encuentra un número B que al multiplicarlo nuevamente por sí mismo da el número A. En forma matemática:
√X = Y donde Y * Y = X
También hay otras formas de definir la raíz cuadrada. Se puede definir en fracción y exponente forma como:
X 1/2 = Y donde Y 2 =X
La raíz cuadrada de un número da dos valores: el número exacto pero de signos opuestos. Por ejemplo, la raíz cuadrada de 4 es +2 y -2 . El +2 se llama raíz cuadrada principal.
Si un número es el área de un cuadrado, entonces su raíz cuadrada dará la medida de uno de sus lados. De manera similar, el cálculo inverso da el área del cuadrado.
Hay dos tipos de raíces cuadradas; perfecto e imperfecto. La raíz cuadrada perfecta es un valor que se resuelve en un número entero como &rad;16 = 4 mientras que un ejemplo de raíz cuadrada imperfecta será &rad;15 = 3,87 .
¿Cómo encontrar la raíz cuadrada?
Por lo general, las calculadoras científicas vienen con el botón de operación de raíz cuadrada. Pero si no tiene acceso a una calculadora, siempre puede utilizar el simplificador de raíces cuadradas en línea.
Es posible calcular la raíz cuadrada a mano, pero los métodos requieren tiempo. Las cuatro formas de encontrar la raíz cuadrada de un número son:
- Método de resta
- División larga
- Método de prueba y error
- Método de factorización prima
Método de resta
En el primer método, reste los números impares en secuencia del valor hasta 0 restos. El número de veces que se resta será la raíz cuadrada. Sólo es aplicable a cuadrados perfectos.
Ejemplo:
Resolver 25 usando este método, primero, resta 1 de eso.
25 - 1 = 24
24 - 3 = 21
21 - 5 = 16
16 - 7 = 9
9 - 9 = 0
El número total de restas realizadas es 5 y esta es la raíz cuadrada.
División larga
El segundo método es el división larga . Es un poco diferente de la división habitual. Comienza dividiendo con el dígito más grande posible. Para el siguiente paso, suma ese coeficiente radical a sí mismo y coloca el valor del cociente junto a él.
Si el coeficiente radical consta de dos dígitos, entonces suma el dígito en el valor posicional más pequeño.
Divide usando este nuevo número y repite hasta que obtengas cero o no sea posible realizar más divisiones.
Ejemplo:
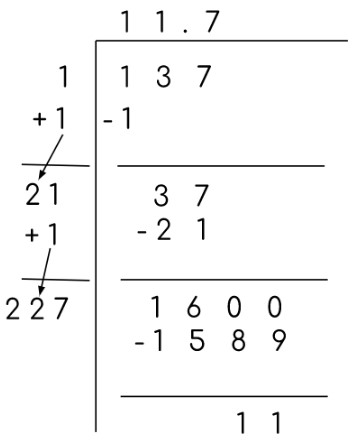
Este es un ejemplo del cuadrado imperfecto que también demuestra que este método puede resolver cuadrados imperfectos.
Método de prueba y error
El tercer método se llama método de prueba y error. Se utiliza en muchos cálculos matemáticos, pero a menudo se omite porque requiere mucho tiempo. Además, debes aprender los cuadrados perfectos para usar esto.
Básicamente, debes adivinar el valor. Ves entre qué dos raíces cuadradas perfectas se encuentra. Como 10 está entre 9 y dieciséis . Entonces su raíz cuadrada debe estar en algún punto entre 3 y 4 Luego luego
Luego notas qué valor está cerca. En nuestro ejemplo, 10 está más cerca de 9 que dieciséis . Entonces, podría ser 3.1 o 3.2 . Tome el cuadrado y verifique.
la plaza de 3.1 es 9.61 y el de 3.2 es 10.24 . Se puede lograr una mayor precisión adivinando el siguiente decimal. digamos que es 3.15 o 3.16 o 3.17 . Tomando al cuadrado los tres tenemos: 9,9225, 9,9856 y 10,0487 . Intentemos encontrar un momento más. Qué pasa 3.162 y 3 .163 . Sus cuadrados son 9.998244 y 10.004567 . Ambos están muy cerca de 10 .
Factorización prima
El cuarto y último método se llama factorización prima porque los factores del número se calculan para obtener su raíz cuadrada. También se utiliza únicamente para cuadrados perfectos.
Los factores se seleccionan por parejas y se resuelven.
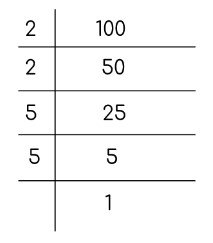
= 2 x 2 x 5 x 5
= 2 2 x5 2
= (2 x 5) 2
= (10) 2
Entonces la raíz cuadrada de 100 es 10.

