To calculate result you have to disable your ad blocker first.
калькулятор пределов
Введите функцию и предел в поля ниже, выберите переменную и нажмите кнопку «Отправить», чтобы решить предел с помощью калькулятор пределов.
Table of Contents:
калькулятор пределов
Oнлайн калькулятор пределов - это онлайн-инструмент, который оценивает пределы для заданных функций и показывает все шаги. Он решает ограничения относительно переменной. Пределы можно оценивать как слева, так и справа, этот решатель пределов.
Какие есть ограничения?
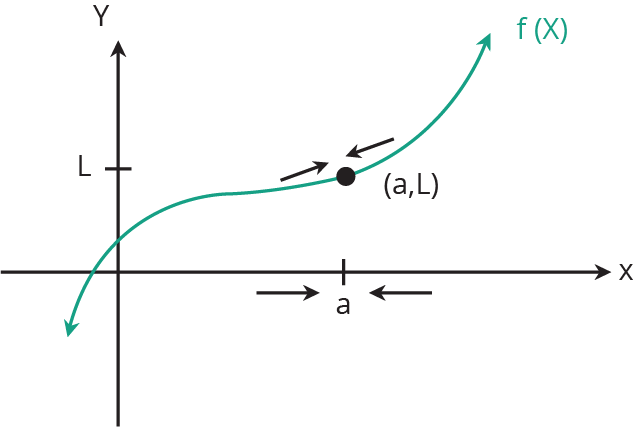
“Предел из функции является значение, f (х) становится ближе к а х приближается некоторое число.”
Пределы жизненно важны для математического анализа и расчетов. Они также используются для определения производных, интегралов и непрерывности.
Как оценить лимиты?
решение пределов онлайн - лучший способ определить пределы, однако мы обсудим ручной метод оценки пределы онлайн. Следуйте приведенному ниже примеру, чтобы понять вычисление пределов онлайн пошаговый метод определения пределов.
Пример:
Найдите предел:
Iimx→2(x3 + 4x2 − 2x + 1)
Решение:
Шаг 1. Примените функцию ограничения отдельно к каждому значению.
= Iimx→2(x3) + Iimx→2(4x2) - Iimx→2(2x) + lIimx→2(1)
Шаг 2: Разделите коэффициенты и выведите их за пределы функции.
= Iimx→2(x3) + 4 Iimx→2(x2) - 2 Iimx→2(x) + Iimx→2(1)
Шаг 3: Примените предел, подставив x = 2 в уравнение.
Iimx→2(x3 + 4x2 − 2x + 1) = 1(23) + 4(22) – 2(2) + 1
Iimx→2(x3 + 4x2 − 2x + 1) = 8 + 16 – 4 + 1
Iimx→2(x3 + 4x2 − 2x + 1) = 21
Указанный выше поиск пределов также использует правило L'hopital для определения пределов.
Часто задаваемые вопросы
Какова концепция калькулятор пределов?
Калькулятор пределов — это онлайн-инструмент, который вычисляет предел заданной математической функции, когда входное значение приближается к определенному значению или бесконечности (в некоторых случаях).
Почему мы используем пределы в математике?
Предел, математическая концепция, основанная на идее приближения, в основном используется для присвоения значений некоторым функциям в точках, где значения не определены, так что они соответствуют близлежащим значениям.
Почему пределы важны в Calc?
Предел сообщает нам значение, к которому будет приближаться функция, когда входные данные функции приближаются к определенному числу. Концепция предела абсолютно фундаментальна как для дифференциального, так и для интегрального исчисления.

