To calculate result you have to disable your ad blocker first.
Rajoituslaskuri
Syötä funktio, muuttuja ja raja alla oleviin kenttiin. Napsauta Laske-painiketta ratkaistaksesi rajan raja-laskimen avulla.
Table of Contents:
Rajoita laskinta vaiheilla
Rajalaskuri on online-työkalu, joka arvioi annettujen toimintojen rajat ja näyttää kaikki vaiheet. Se ratkaisee muuttujan rajat. Rajat voidaan arvioida joko vasemmalla tai oikealla puolella käyttämällä tätä rajaratkaisijaa.
Mitkä ovat rajat?
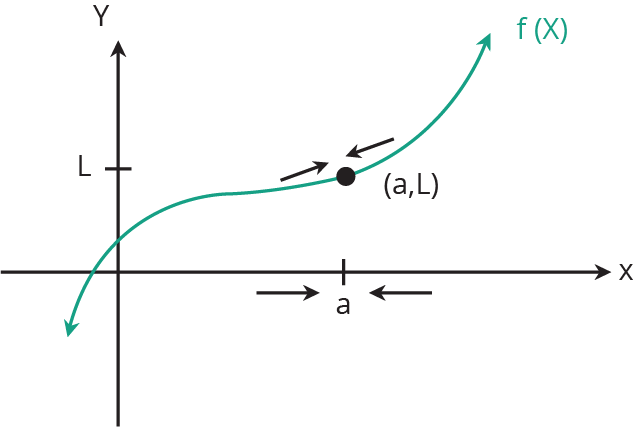
” Raja on funktio on arvo, joka f (x) saa lähempänä kuin x lähestymistapoja joidenkin numero. ”
Rajat ovat elintärkeitä matemaattiselle analyysille ja laskennalle. Niitä käytetään myös johdannaisten, integraalien ja jatkuvuuden määrittelemiseen.
Kuinka arvioida rajoja?
Raja-arvioijan käyttö on paras tapa ratkaista rajat, mutta keskustelemme manuaalisesta menetelmästä rajojen arvioimiseksi. Seuraa alla olevaa esimerkkiä ymmärtääksesi vaiheittaisen menetelmän rajojen ratkaisemiseksi.
Esimerkki:
Iimx→2(x3 + 4x2 − 2x + 1)
Ratkaisu:
Vaihe 1: Käytä rajatoimintoa erikseen kullekin arvolle.
= Iimx→2(x3) + Iimx→2(4x2) - Iimx→2(2x) + lIimx→2(1)
Vaihe 2: Erota kertoimet ja poista ne rajatoiminnosta.
= Iimx→2(x3) + 4 Iimx→2(x2) - 2 Iimx→2(x) + Iimx→2(1)
Vaihe 3: Käytä rajaa korvaamalla yhtälössä x = 2 .
Iimx→2(x3 + 4x2 − 2x + 1) = 1(23) + 4(22) – 2(2) + 1
Iimx→2(x3 + 4x2 − 2x + 1) = 8 + 16 – 4 + 1
Iimx→2(x3 + 4x2 − 2x + 1) = 21
Yllä oleva rajahaku käyttää myös L'hopitalin sääntöä rajoitusten ratkaisemiseen.

