Калькулятор теоремы Пифагора

Калькулятор теоремы Пифагора

Калькулятор теоремы Пифагора — это помощник по геометрии. Он использует Пифагора’ формула нахождения трех сторон прямоугольный треугольник . Вы можете найти гипотенуза или любая из двух других сторон.

Как пользоваться калькулятором теоремы Пифагора? 

Следуйте инструкциям ниже.

1. Выберите сторону треугольник вы хотите найти, например. гипотенуза. 
2. Введите значение двух других стороны .
3. Нажмите вычислить .
4. Результат появится через секунду.

Вы можете использовать его несколько раз бесплатно, сбросив калькулятор.

Что такое теорема Пифагора?

Слово Пифагорейский принадлежит известному греческому ученому Пифагор который впервые доказал эту теорему. В нем говорится, что :

“ площадь площади сторона которого является гипотенузой (стороной, противолежащей прямому углу), равна сумме области квадратов на двух других сторонах».

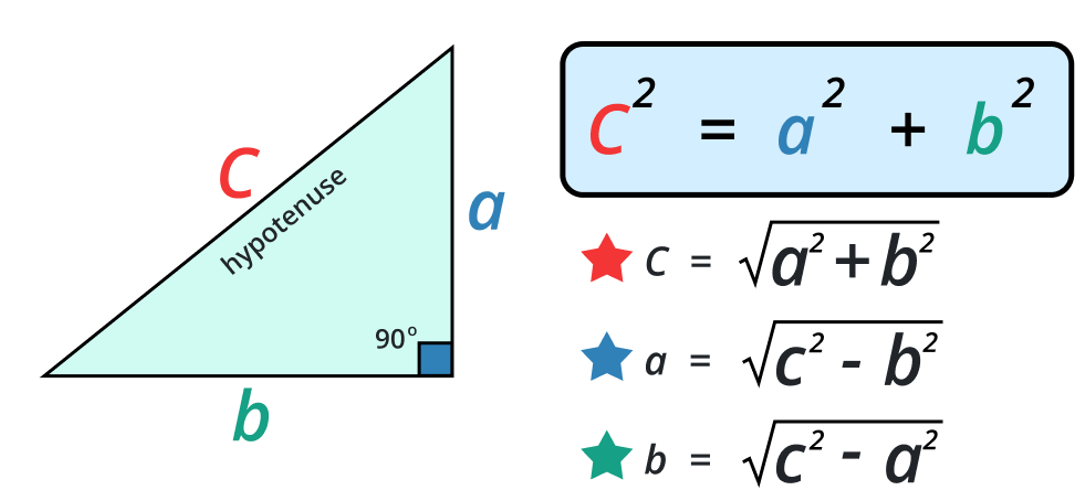
Его можно использовать для вывода уравнения гипотенузы, в котором гипотенуза равна нижнему корню. сумма квадратов двух других длин. Это написано как:

с 2 = а 2 + б 2  

Где с — длинная сторона, противоположная прямому углу, известному как гипотенуза. Письмо а обычно представляет собой прилегающую сторону и букву б представляет другую сторону.

Это уравнение также известно как уравнение Уравнение Пифагора .

Формулы трех частей уравнения Пифагора

Уравнение можно составить так, чтобы найти длину любой стороны.

• Для гипотенузы: &радик; (а 2 + б 2 )

• Для стороны А: &радик;(б 2 - c 2 )
• Для стороны Б: &радик;(а 2 - с 2 ) 

Нахождение сторон по теореме Пифагора

Никогда не помешает увидеть пример, не так ли!?

Пример:

Найдите недостающую сторону следующего треугольник .

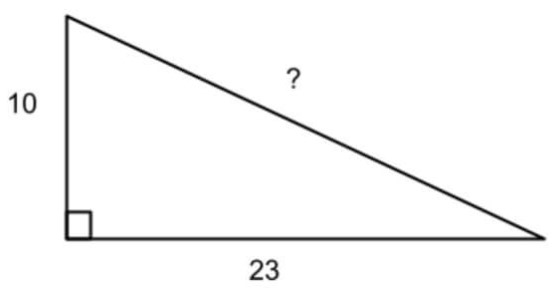
Решение:

Шаг 1: Определите данные данные.

а = 10

б = 23

Шаг 2: Поместите в Уравнение Пифагора .

с 2 = а 2 + б 2

с ² = (10) ² + (23) ²

с ² = 100 + 529

с 2 = 629

Шаг 3: Извлеките квадратные корни с обеих сторон.

с = &радик;629

с = 25.1