Greatest Common Factor: Definition, Methods, & Calculations

The greatest common factor (GCF) is an important concept and a core dimensional topic in the study of mathematical operations especially in solving real-world problems. It plays a key role in simplifying fractions and determining the common denominators.

Before discussing the concept of the greatest common factor, it is important to apprehend the concept of factors. The natural numbers that can be divided and we get an answer without leaving a remainder are known as factors.

In this article, we’ll explore the concept of the greatest common factor (GCF) along with its methods for computing the GCF, applications, and solved examples.

What is the Greatest Common Factor (GCF):

The greatest common factor can be defined as the greatest positive number that divides two or more numbers without leaving a remainder. It is the highest value that can evenly divide each of the given numbers. It is employed to determine the common multiples and simplify the fractions.

The greatest common factor is also termed the Greatest Common Divisor (GCD) and highest common factor (HCF).  

Methods to Determine GCF

The greatest common factor can easily be computed by using the following methods:

• List of Factors Method
• Prime Factorization Method
• Division method

List of Factors Method

In this method, we’ve to write down all the factors/divisors of the given numbers. After listing down the divisors of the given numbers, we’ve to choose the greatest number that divides the given numbers without leaving any remainder which is the GCF or the highest common divisor.

This method is beneficial for determining the GCF of the given numbers. Such as the GCF of 30 & 42

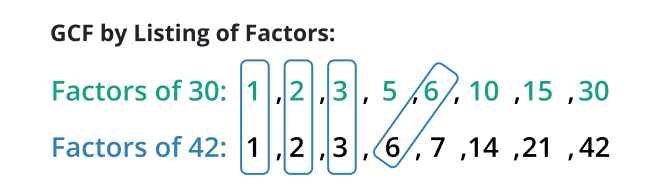
Hence, 6 is the GCF of 30 & 42.

Prime Factorization Method

In this method, we’ve to find out the prime factors of the given numbers and sort out the common prime factors.  Then common prime factors are multiplied together to get the greatest common factor.

Let us discuss the GCF of 24 and 30 using the prime factorization.

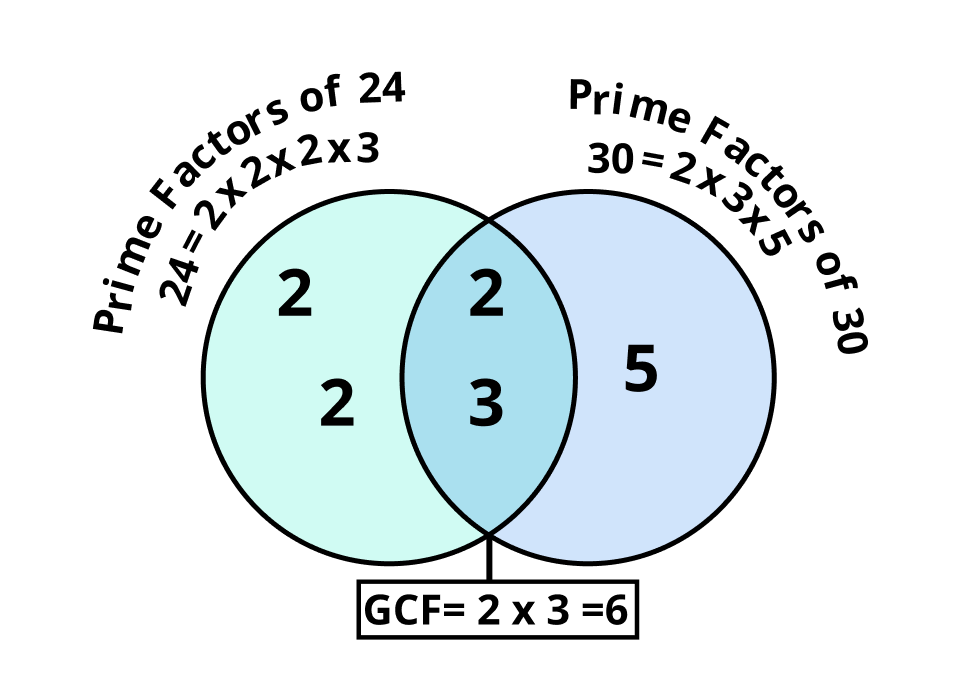
Method of Long Division:

In this method, we’ve to divide the larger number by the smaller number using the method of long division so that the remainder becomes zero. If the remainder is zero, then the divisor is known as the GCF which is the last non-zero residue.

If the remainder is not zero, then we choose the remainder of the predecessor (previous) step as the divisor and the divisor of the previous step as the dividend. We perform the long division method again and again until we get zero as the remainder. Therefore, in this way, the divisor of the last division is considered the GCF of the given two numbers.

How to find the greatest common factor?

Below are a few examples for determining the GCF.

Example 1:

Find the GCF of 20 & 28 by using the list of factors method.

Solution:

Step 1: Given data,

Numbers: 20 and 28

Step 2: Make factors of the numbers:

Factors of 20: 1, 2, 4, 5, 10, 20

Factors of 28: 1, 2, 4, 7, 14, 28 

Step 3: Observe and note down the common factors of 20 & 28.

Common factors = 1, 2, 4

Greatest common factor = 4

Hence, 4 is the GCF of 20 & 28.

Example 2:

Compute the GCF of 56 and 84 using Prime Factorization.

Solution:

Step 1: Given data,

Numbers: 56 and 84

Step 2: Prime factorization of numbers:

Prime factors of 56: 2 x 2 x 2 × 7

 Prime factors of 84: 2 x 2 × 3 × 7

Step 3: Write common factors

Common prime factors = 2, 2, 7

Greatest common factor = 2 x 2 × 7 = 28

Therefore, the GCF of 56 and 84 is 28.

Example 3:

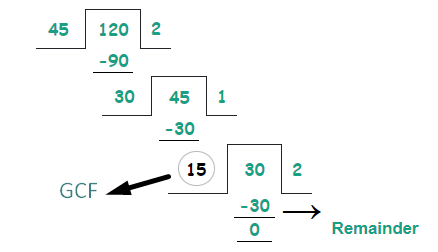
Determine the GCF of 45 and 120 by using the division method.

Solution:

Step 1: Given information:

Numbers: 45, 120

Step 2: We take the larger value 120 as a dividend and the smaller value 45 as a divisor.

Applications of the GCF:

The concept of the greatest common factor is very useful in different mathematical problems. Let us explore some important applications of GCF.

Simplifying Fractions:

GCF plays an important role in simplifying the fractions. This method reduces the fractions to their simplest form, simplifies calculations, and allows for comparisons between fractions.

In this method, we divide both parts of a fraction (numerator & denominator) by their GCD. By dividing both the numerator and the denominator of a fraction by their GCF, we can obtain an equivalent fraction in simplified form.

Determining Common Denominators:

GCF is crucial in determining a common denominator by adding or subtracting fractions with discrete denominators. The GCF helps us to determine the smallest common multiple of the denominators, empowering us to determine equivalent fractions with the same denominator.

GCF in Prime Factorization:

Prime factorization is an important and significant method to find the GCF. By writing the given numbers as a product of their prime factors, we can obtain the common prime factors to determine the GCF.

GCF in Algebraic Expressions:

The greatest common factor is not only applicable to whole numbers but also explores algebraic expressions, especially the topics of linear algebra as well.

In algebra, the GCF can be divided evenly into every term of the expression. By factoring out the GCF, we can simplify the complex expressions and make further calculations easy.

Conclusion:

The Greatest Common Factor (GCF) is a vital mathematical concept that helps us find the largest number by dividing evenly into two or more given numbers. In this article, we have addressed the core dimensional concept of the greatest common factor and methods for the computation of the GCF as well as its important applications.