Disjunction: Definition, Uses, Applications, and Examples

Disjunction is a fundamental concept in mathematics that deals with logical reasoning and set theory. It represents the notion of either/or at least one in various contexts. Disjunction is essential to problem-solving and decision-making in all situations and covers logic, probability, mathematics, and real occurrences.

What is Disjunction?

A disjunction is a term for the link created by an “OR” gate between two sentences. Only the combined compound statement about disjunction is valid when at least one of the statement will be true. We may read our two statements as circles are curves and parallelograms are oval.

To combine them into one statement, use the disjunction “OR” to create the compound sentence “circles are curves OR parallelograms are ovals.” The new compound statement is only true if the preceding at least one proposition is true. If merely two of the statements are false then the compound statement will not be true.

Understanding Propositions

Becoming familiar with the concept of propositions is essential before moving on to the study of disjunction. An uncertain statement is referred to as a proposition.

e.g.,

It is raining outside and 2 + 2 = 5 are propositions. Disjunction helps us analyze and evaluate the relationship between these propositions.

Where we can use the disjunctions?

The fields where we can use disjunctions are as follows:

• Disjunction in Logic
• Disjunction in Sets
• Disjunction in Probability
• Disjunction in Algebra
• Disjunction in Computer Science

Disjunction in Logic

In logic, disjunction is an operator denoted by the symbol “∨” logical OR. A compound proposition is formed when two statements are made, and it is true if at least one of the original claims is true. 

e.g.,

Prepositions p and q can only be disjunctuated if at least one of them is true. The compound statement will be valid if it is demonstrated that both prepositions are true.

Disjunction in Sets

In set theory, disjunction refers to the union of sets. The union of two sets A and B represents the set containing all elements in either A or B or both and is denoted by A ∪ B.

e.g.,

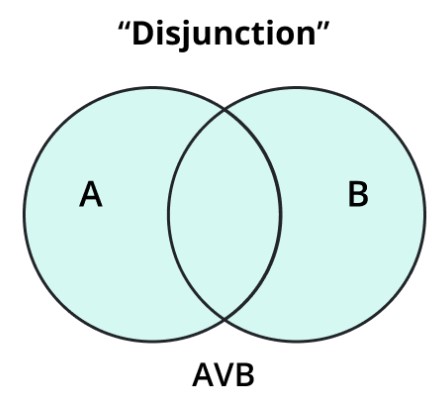
if A = {1, 2, 3} and B = {3, 4, 5}

then A ∪ B = {1, 2, 3, 4, 5}.

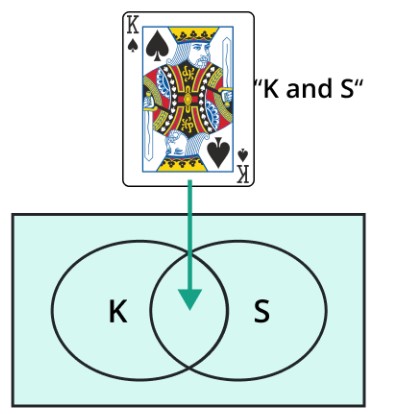
Disjunction in Probability

P (K V S) = P(K) + P(S) - P (K ∧ S), where P(K) denotes the likelihood of event K, P(S) denotes the likelihood of event S, and P (K V S) denotes the chance of both events occurring, is the formula for the probability of the disjunction of two occurrences K and S.

Disjunction in Algebra

Algebraic disjunction has to deal with the concept of inequality.

e.g.,

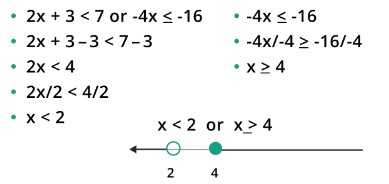
The disjunction 2x + 3 < 7 ∨ -4x ≤ -16 is used to describe the collection of all points x, x that meet either x < 2 or x ≥ 4.

It helps us examine specific coordinate plane regions and appreciate the connections between variables.

Disjunction in Computer Science

In computer science, disjunction is widely used in programming and Boolean logic. Boolean variables can take on two values: 0 or 1.

e.g.,

Disjunction allows programmers to create conditional statements and control structures that execute specific code blocks based on the evaluation of disjunctive conditions.

Disjunction in Decision Making

A disjunction is an essential tool in decision-making, as it allows us to explore colorful possibilities and estimate different options. Understanding the connections between propositions and their disjunctions allows us to make informed choices that optimize issues.

Disjunction in Mathematics Education

Disjunction is an important mathematical topic because it improves students’ ability to think logically and solve problems. Students may evaluate complex subjects, divide them into simpler parts, and establish logical conclusions through understanding disjunction.

Challenges and Limitations of Disjunction

While disjunction is a powerful tool, it also has its limitations. One challenge is the potential for oversimplification or overlooking crucial factors when reducing complex situations to binary choices. Disjunction alone may not capture the full complexity of certain scenarios requiring more refined reasoning.

Disjunction in Real-Life Scenarios

Disjunction finds practical applications in numerous real-life scenarios. It enables decision-making processes, such as choosing between different options or assessing multiple conditions simultaneously.

e.g.,

In medical diagnostics, disjunction can help identify potential diseases based on a combination of symptoms.

Example of Disjunction

Keep the given general statements A and B together to make a disjunction.

A:  The sun is shining.

B: It is raining.

Solution

The disjunction of A and B is as follows

A V B: The sun is shining OR It is raining.

The truth table for the above-mentioned example is as follows:

Wrap up

A fundamental concept in mathematics called disjunction is essential in a variety of situations. In several disciplines, including probability, mathematics, computer science, logic and set theory, and probability, disjunction helps in connection analysis, conclusion formulation, and problem resolution.