To calculate result you have to disable your ad blocker first.
Inverse Matrix Calculator
To find the inverse of matrix, choose the order of the matrix, input the entries of the matrix, and click calculate button
Matrix Inverse Calculator
Inverse matrix calculator solves a matrix to find its reverse using the elementary row and column elimination. It will give the whole process of finding the inverse of the matrix.
What is the inverse of the matrix?
The reverse of the original matrix is called its inverse. It is often denoted by A-1. When a matrix is multiplied by its inverse, it gives the identity matrix. This trick can help to verify the accuracy of the inverse matrix.
Matrix inverse formula:
The formula used for the inverse matrix is:
A-1 = (1/ |A|) . adj A
Where
- |A| is the determinant of the matrix A.
- Adj A means adjoint of A. It is found using transpose.
This formula helps in a 2x2 square matrix better. For 3x3 or bigger matrices, mostly the elementary transformation is used.
How to calculate the inverse of a matrix?
There are basically four methods, two of which are discussed above. The list of these methods is:
- Inverse matrix calculator.
- Using the formula.
- Elementary transformations.
- Finding the cofactors.
The calculator uses the second last method. There are two ways to carry out this transformation; row elimination and column elimination. The rows are subtracted or added and multiplied to each other and in some cases both.
- Write the equation A=I.A, where I is the identity matrix of the same order.
- The transformation will be applied on the A at the LHS and I on the RHS. the A on the RHS will remain intact.
- Perform different techniques on the Left-hand side A to make it an identity matrix. Make the same changes to the identity matrix regardless.
- When the A has become the identity matrix, the original identity matrix I would now be different and called matrix B. That is I=BA.
- I=BA is equal to A-1=B, hence B is the inverse of matrix A.
Example: (row elimination)
Find the inverse of the following matrix:
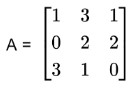
Solution:
Step 1: Write the formula.
A=l.A
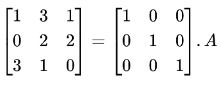
Step 2: Subtract the R1 multiplied by 3 from R3.
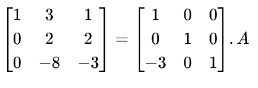
Step 3: Divide R2 by 2.
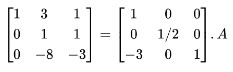
Step 4: Subtract R2 multiplied by 3 from R1.
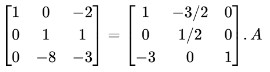
Step 5: Multiply R2 by 8 and add it to R3.
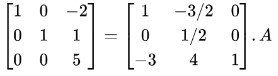
Step 6: Divide R3 by 5.
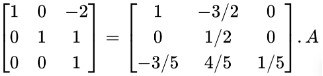
Step 7: Multiply R3 by 2 and add it to R1.
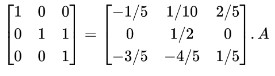
Step 8: Subtract R3 from R2.
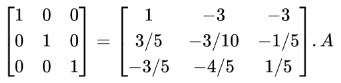
An identity matrix on LHS is obtained. Hence I = BA or A-1 = B.

