Fractals: Definition, Types, Examples, & Applications

In this article, we’ll explain the definition, types, and applications of fractals. Let’s unravel the mysteries of this topic.

What are fractals?

Fractal is a pattern that never ends. It elaborates mathematical constructs that exhibit self-similarity, meaning they display similar patterns or structures when zoomed in or out.

This self-similarity occurs at many levels of magnification, revealing elaborate details that are replicated at every scale. Fractal geometry deals with complexity and irregularity.  While on the other hand, traditional Euclidean geometry, deals primarily with simple shapes such as circles, squares, and triangles.

Types of fractals:

Fractals have three basic types which are below.

1. Self-similar fractals
2. Self-affine fractals
3. Invariant fractals

Now we explain all of them briefly.

Self-Similar Fractals

Self-similar fractals have parts as scaled-down versions of the entire object. we can construct the object by applying different scaling factors to all parts or by using the same scaling factor for all. If we use a random scaling factor to generate subparts fractals are called statistically self-similar.

This is used to construct shapes like trees and plants etc.

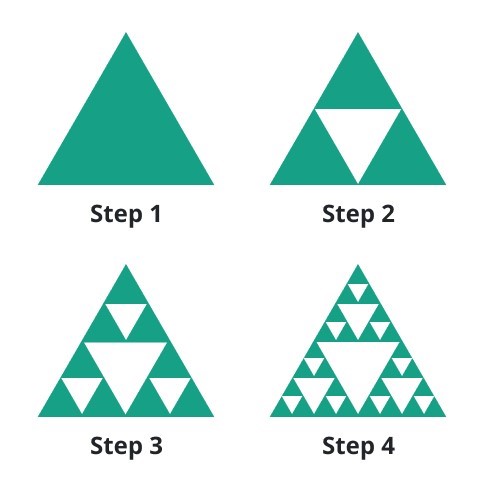
A classic example of a self-similar fractal is the Sierpinski triangle, where smaller triangles within the larger triangle are identical in shape.

Self-Affine Fractals

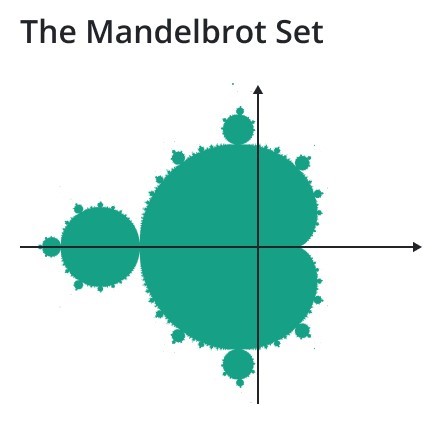
Self-affine fractals use different scaling factors for all three directions. We can add random variation to get statistically self-affine fractals that are used to model terrain, water, clouds, etc. A classic example of a self-affine fractal is the famous Mandelbrot set, which exhibits intricate and infinitely complex patterns when zoomed in.

Invariant Fractals

Invariant fractals are categorized by their invariable nature under specific transformations. Rotation, translation, and scaling may be included in this transformation. Invariant fractals retain their overall shape and structure regardless of these transformations.

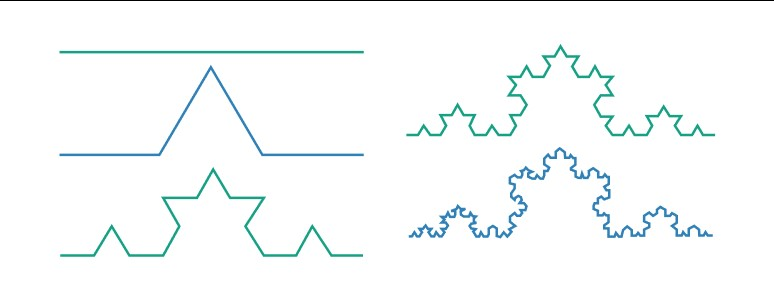
An example of an invariant fractal is the Koch snowflake, which maintains its overall shape even when subjected to transformations such as rotating or scaling.

Examples of Fractals

There are many famous examples of fractal but here we take only two

1. Sierpinski triangle
2. Koch (Triadic) Curve in

 Example 1: Sierpinski triangle

We have a different fractal and calculate its self-similarity dimension. The fractal we’ll consider now is a famous fractal known as the Sierpinski triangle. Here are the steps in its construction

1. Starts with the solid triangle.
2. Divide the triangle into four smaller triangles congruent triangles by connecting the midpoint of each side.
3. Removed the middle triangle.
4. Repeat steps 2 and 3 until we get a fractal as shown in the last image.

So, it is a fractal because we see these triangles within triangles, within triangles repeating in many different scales itself similar.

Example 2:( Koch (triadic) curve)

Here are the steps to construct the famous fractals Koch curve.

1. Take a line segment.
2. Divide a line into three equal parts.
3. Place the equilateral triangle on the middle point and remove the baseline of the middle part. Now the curve has four segments.
4. Divide each segment into 3 equal parts.
5. Repeat step 2

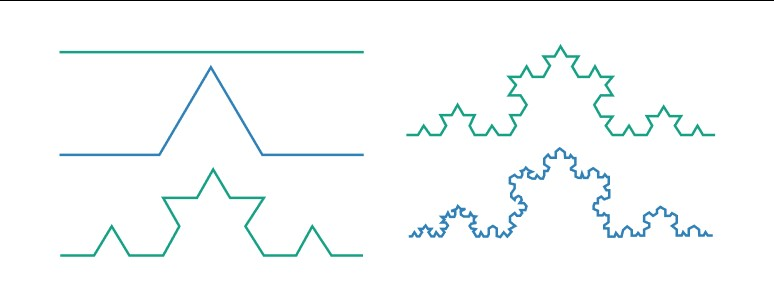
This repetition goes on for an infinite time if we zoom any section of the curve, the basic triangle structure can be seen.

Applications of Fractals

Fractals possess many applications in various fields.  Let’s discuss some noteworthy applications from them.

Fractals in Computer Graphics

We used fractals in computer graphics to generate realistic landscapes, textures, and natural phenomena. They provide a powerful tool for creating intricate and visually captivating virtual environments.

Data Compression

We used fractals in data compression and data compression is a technique that offers efficient ways to compress and store digital data, particularly images. By exploiting the self-similarity present in images, fractal-based algorithms can compress data while preserving visual quality.