To calculate result you have to disable your ad blocker first.
Dimensions in Mathematics: Definition, Types, Applications, and Examples

Publish Date: 13 Nov, 2023
Table of Content
Have you ever wondered how mathematicians deal with dimensions? We will claw into the absorbing domain of dimensions and how they impact calculations in this blog composition.
We will look at the numerous aspects of dimensions and how they could be applied in some factual situations. So, let's dive in and discharge the distraction of dimensions!
What is a Dimension?
The lowest set of coordinates that may be used in mathematics to describe a point in space is called a dimension.
It provides a measure of the extent or size of an object or space along a particular axis. Dimensions help us understand the structure and properties of mathematical objects.
Typically, dimensions are represented as
- Length
- Breadth
- Width
- Height or depth
Understanding Mathematical Dimensions
Mathematical dimensions come in a wide variety of forms, similar to geometric, topological, and fractal dimensions. Geometric dimensions, the most common type, are usually related to actual places.
Topological dimensions focus on the connectedness and continuity of spaces, while fractal dimensions describe complex and self-similar patterns.
The Importance of Dimensions in Math
In multiple fields of mathematics, like geometry, calculus, and algebra, dimensions are essential. They give a structure for understanding and describing things and phenomena.
By considering different dimensions, mathematicians gain insights into the behavior of mathematical structures and solve real-world problems.
Types of Dimensions
The most commonly used types of dimensions are as follows:
- One-Dimensional Space
- Two-Dimensional Space
- Three-Dimensional Space
- Higher Dimensions
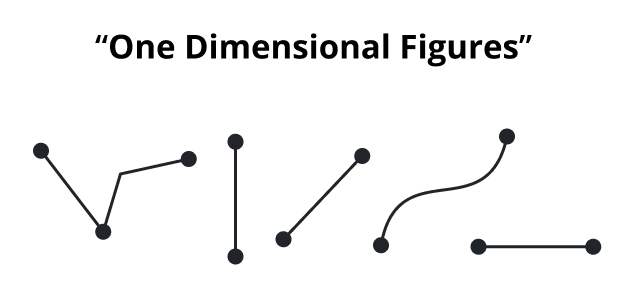
One-Dimensional Space
Let's start our exploration by understanding one-dimensional space. A 1D space refers to a line, where points can only move along a single axis. It is neither broad nor deep; it is merely long. Objects with only one dimension include wires, lines of straight, and number lines.
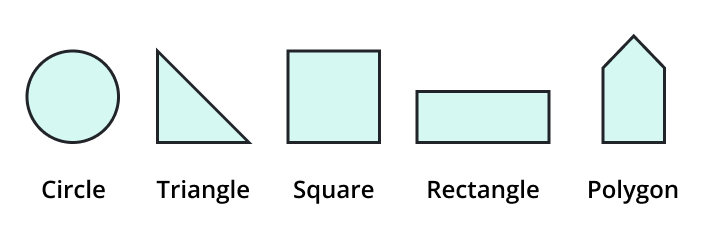
Two-Dimensional Space
There is a plane or flat surface in 2D space. Objects may move freely on the plane in 2D space because it contains width in addition to length, unlike 1D space, which only has length. Examples of 2D goods include places, circles, triangles, and any flat form.
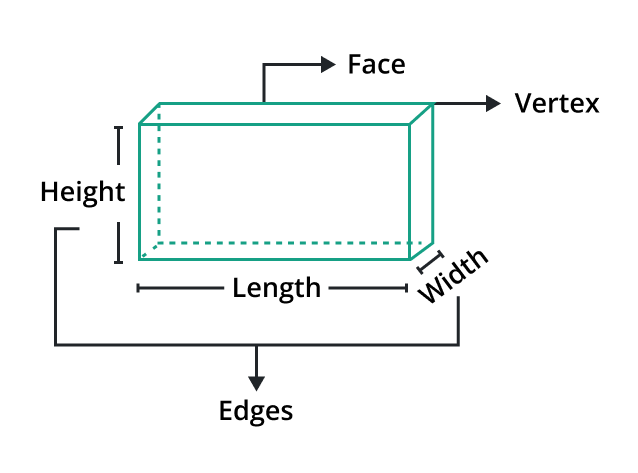
Three-Dimensional Space
It allows objects to have volume and enables movement along three axes. Our physical world is an excellent example of 3D space, where we experience objects with length, width, and height.
Higher Dimensions
While our everyday experience is limited to three dimensions, mathematics goes beyond these boundaries. Higher dimensions refer to spaces that involve more than three axes.
Although visualizing higher dimensions can be challenging, mathematicians use abstract representations and mathematical formulas to comprehend and study them. These higher dimensions play a vital role in fields like string theory and advanced geometry.
Dimensional Analysis
In addition to spatial dimensions, we have dimensional analysis, a powerful tool used in various scientific and engineering disciplines. Dimensional analysis involves examining the dimensions of physical quantities and their relationships to solve complex problems.
It helps ensure the consistency and accuracy of mathematical equations and calculations.
Fractals and Dimensions
Fractals, fascinating mathematical objects, blur the boundaries between dimensions. They possess fractional dimensions, which lie between whole numbers. Fractal dimensions capture the intricate self-similarity and complexity found in natural phenomena like coastlines, clouds, and biological structures.
Fractal geometry plays a crucial role in computer graphics, data compression, and modeling natural systems.
Practical Applications
Dimensions have practical applications in diverse fields.
- Architecture and engineering
- Physics
- Computer graphics
Architecture and engineering
Understanding dimensions is essential for designing structures and creating blueprints.
Physics
In physics, dimensions are fundamental to describing the behavior of particles and systems.
Computer graphics
Dimensions are also integral to computer graphics, virtual reality, and data visualization, where three-dimensional representations enhance user experiences and understanding.
Examples
Quality Examples for Dimensions are as follows:
Example 1:
What is the number of dimensions in the given figure?

Result:
The figure has just one dimension, and length, and is composed of a curved line connecting two points.
Example 2:
What number of dimensions does the provided figure have?

Result:
Either a dot or a point, depending. It lacks all dimensions, not even length and width.
Example 3:
How many dimensions does a scale possess?
Result:
A scale's length, breadth, and thickness. As a result, it seems to be three-dimensional.
Example 4:
A cylindrical water bucket has how many dimensions?
Result:
A cylinder has the following measurements: height, depth, and width. As a result, it has three dimensions.

