Acute Triangle: Definition, Types, and Examples

The idea of acute triangles has been around for a long time, and people in various cultures who were interested in math and astronomy probably studied these kinds of triangles. Acute triangles also had an impact on the creation of trigonometry, which is a branch of math that looks at how the sides and angles of triangles are connected to each other.

In this article, we will discuss the definition of the acute triangle and its properties and solve some examples for better understanding.

What is the acute triangle?

An acute triangle is a type of triangle where all three angles are less than 90 degrees. In other words, an acute triangle has acute angles and no flat angles.

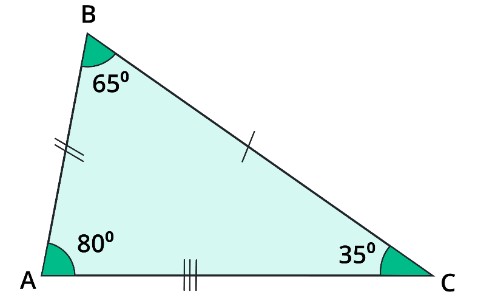
For example, the given image is the acute triangle with 35^o, 65^o, and 80^o angles.

Types of acute triangles:

You might be curious as to how many different kinds of acute triangles there are:

• The acute triangle with equal sides.
• The acute isosceles triangle
• The acute scalene triangle

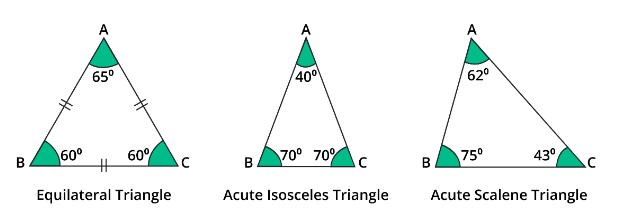
Acute Equilateral Triangle:

An acute triangle with all interior angles of 60° is considered equilateral.

Acute isosceles triangle:

An acute isosceles triangle is a type of triangle in which two angles and both sides are equal, and the angles are acute. For example, two angles in an acute isosceles triangle might be 70 degrees.

Acute Scalene Triangle:

The acute scalene triangle is a type of triangle in which the three angles are different and the three sides are different lengths. Also, all angles of an acute triangle are less than 90 degrees.

Acute Triangle Features:

In general, the characteristic of an acute triangle is that all interior angles are less than 90 degrees:

• An acute triangle's angles must all add up to 180 degrees according to the Angle Sum Property.
• The triangle's smallest side is the one that faces the smallest angle.
• A triangle cannot have both straight and acute angles.
• The total of the squares with two smaller sides is less than the square with the longest side.
• Obtuse and sharp angles cannot coexist in the same triangle.
• Any triangle with an angle larger than 90° is said to be obtuse.

Application of the acute triangle:

Acute triangles have various applications in different fields.  Here are some examples:

• Acute triangles are fundamental shapes in geometry and serve as building blocks for many geometric constructions.
• These functions are extensively used in fields like physics, engineering, and architecture for calculations involving angles and distances.
• Engineers and architects use acute triangles to calculate load distributions, angles of inclination, and other geometric properties relevant to their designs.
• Acute triangles find applications in navigation and surveying, especially in determining distance and angles.
• They are often used to approximate complex shapes and provide efficient calculations for game physics and graphics.

Formulas of an acute triangle:

There are two different formulas used to calculate the area and perimeter of the acute triangle:

• Area of an acute triangle
• The perimeter of an acute triangle

Area of the acute triangle:

The basic formula for the calculation of the acute triangle is defined as,

Area = (1 / 2) * b * h

Here

• b = base of the acute triangle
• h = height of the acute triangle

if all three sides of the triangle are given then we can also use Heron’s formula

Case 1: all sides are given

Heron’s formula:

Area = √S (S – a) (S – b) (S – c)            square units

Here,

• S = (a + b + c) / 2
• a, b, and c are the sides of the triangle.

Case 2: two sides and interior angle is given

Area = (1 / 2) * ab * sin C

OR

Area = (1 / 2) * bc * sin A

OR

Area = (1 / 2) * ca * sin B

Here,

• a, b, and c are sides of the triangle,
• A, B, and C are the interior angle of the triangle

The perimeter of the acute triangle:

The perimeter of a triangle is equal to the sum of the three sides of the triangle.

Perimeter = a + b + c   units

Examples

Here are the examples for better understanding:

Example 1:

Find the area of an acute triangle having sides 6, 12, and 14.

Solution:

Step 1: Extract data

a = 6

b = 12

c = 14

step 2: Write the formula

here we have all three sides of the triangle then we use Heron’s formula to calculate the Area of the triangle

Area = √S (S – a) (S – b) (S – c)             square units

Step 3: Find “S”

S = (a + b + c) / 2

S = (6 + 12+ 14) / 2

S = 32 / 2

S = 16

Step 4: Find (S – a), (S – b), and (S – c)

(S – a) = 16 – 6 = 10

(S – b) = 16 – 12 = 4

(S – c) = 16 – 14 = 2

Step 5: Put value in Heron’s formula

Area = √ (16) * (10) * (4) * (2)            square units

Area = √1280                                       square units

Area = 16√5    square units

Wrap up:

In this article, we discussed the concept of the acute triangle and its history of invention. We analyzed the different types of acute triangle and their properties and applications in our daily life.

Here we can also study the different methods to calculate the area of the acute triangle i.e., the Area of an acute triangle and the perimeter of an acute triangle.