To calculate result you have to disable your ad blocker first.
Basics of Additive Inverse with its Types and Applications
Publish Date: 08 Aug, 2023
Table of Content
Mathematics, with its intricate web of theories and principles, often presents us with fascinating concepts that unlock the secrets of numerical relationships. The additive inverse is one such concept that enhances our understanding of addition and subtraction.
Discover the concept of the additive inverse and its significance in mathematics. Dive into the world of mathematical operations and learn how the additive inverse complements addition and subtraction. Explore FAQs, examples, and more in this comprehensive guide.
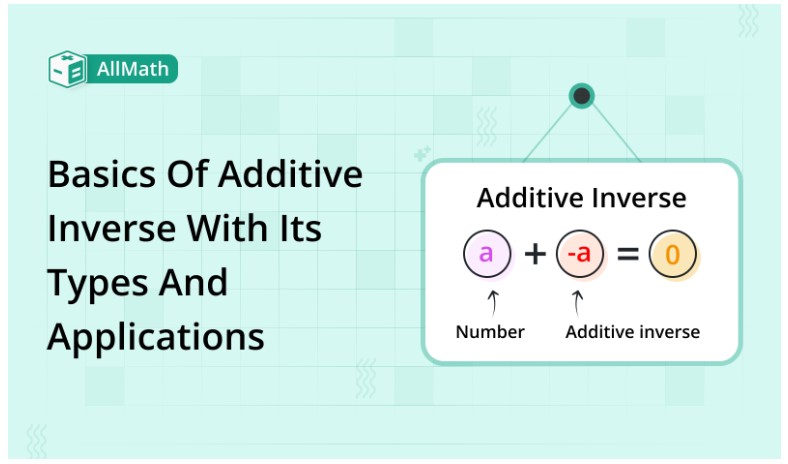
What is the Additive Inverse?
The additive inverse, also known as the opposite /negation, is a fundamental concept in mathematics. It describes a number that, when added to another, produces the result of zero. In simpler terms, it is the number that "undoes" the effect of addition, bringing us back to the neutral starting point.
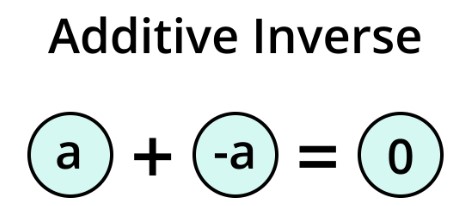
Significance of the Additive Inverse
The additive inverse serves as a critical component in various mathematical operations and theories. By understanding its significance, we can delve deeper into the realm of numbers and uncover their interconnectedness.
Additive Inverse and Subtraction
Subtraction, an operation closely related to addition, relies on the concept of the additive inverse. It is similar to adding the additive inverse of the number being subtracted when we subtract one integer from another. This connection allows us to perform subtraction with ease and expand our mathematical capabilities.
Uniting Addition and Subtraction
The additive inverse bridges the gap between addition and subtraction, forming a cohesive unit in the realm of mathematical operations. With the knowledge of the additive inverse, we can seamlessly transition between the two operations, enhancing our problem-solving skills and mathematical fluency.
The Applications of the Additive Inverse:
Now that we have gained a basic understanding of the additive inverse, let's explore its practical applications in various mathematical scenarios. From solving equations to deciphering real-world problems, the additive inverse finds its utility in numerous contexts.
Solving Equations
Equations often present us with unknown variables that require careful manipulation to find their values. We can isolate a variable and establish its precise value by adding the additive inverse of a term to both sides of an equation.
Balancing Scales
Think of a scale with weights on both sides. We must guarantee that both sides are balanced to establish equilibrium. The additive inverse helps us achieve this balance by adding the opposite weights to each side of the scale, ultimately leveling it out.
Vector Operations
In the realm of vectors, the additive inverse finds its place in operations such as vector addition and subtraction. By adding the additive inverse of a vector, we can negate its effects and alter the overall direction and magnitude of the resultant vector.
Financial Transactions
In the world of finance, the additive inverse manifests itself in the concept of income and expenses. Positive values represent income, while negative values denote expenses. By employing the additive inverse, we can accurately calculate net profits or losses and make informed financial decisions.
FAQs
Q 1: What use does the additive inverse in mathematics serve?
The additive inverse serves as a fundamental concept that complements addition and subtraction. It allows us to undo the effects of addiction and navigate the realm of mathematical operations with greater ease and flexibility.
Q 2: How can I determine a number's additive inverse?
If the number is positive, make it negative, and if it is negative, make it positive. The result is the additive inverse of the initial number.
Q 3: Can a fraction or a decimal represent the additive inverse?
Yes, including both decimals and fractions in any real number can serve as the additive inverse. The concept applies to all types of numbers, irrespective of their form.
Q 4: Are zero and zero's additive inverses the same?
When zero is added to any number, the result remains unchanged. It acts as a neutral element in the realm of addition and subtraction.
Q 5: How does the additive inverse relate to multiplication and division?
The additive inverse primarily applies to addition and subtraction. It does not have a direct connection to multiplication and division, which involve their distinct concepts, such as the multiplicative inverse or reciprocal.
Q 6: Can you provide an example showcasing the additive inverse in action?
Certainly! Let's take the number 5. Its additive inverse is -5. When we add 5 and -5, the result is zero, indicating the cancellation of the two numbers.
Conclusion
In this article, we've discussed the additive inverse and its applications in various mathematical scenarios. By grasping this concept, we can confidently navigate the mathematical landscape, exploring its shade and expanding our problem-solving abilities.

